Σύγκριση και διάταξη κλασμάτων

17

Διερεύνηση

Τα παιδιά έχουν χωριστεί σε ζευγάρια και παίζουν ένα ηλεκτρονικό παιχνίδι.

α. Ο ήρωας του Νίκου έχει καλύψει τα $\dfrac{4}{7}$ της πίστας-διαδρομής και του Αντρέι τα $\dfrac{5}{7}$ .

β. Ο ήρωας της Αγγελικής έχει καλύψει τα $\dfrac{2}{17}$ της πίστας-διαδρομής και της Δανάης τα $\dfrac{2}{19}$ .

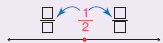
γ. Ο ήρωας του Ορέστη έχει καλύψει το $\dfrac{1}{2}$ της πίστας-διαδρομής
και της Κέλλυ τα $\dfrac{17}{31}$ .

δ. Ο ήρωας του Σπύρου έχει καλύψει τα $\dfrac{16}{27}$ της πίστας-διαδρομής
και της Λίας τα $\dfrac{18}{24}$ .

Ποιος ήρωας έχει καλύψει τη μεγαλύτερη διαδρομή σε κάθε ζευγάρι;

Συγκρίνουμε τα κλάσματα (<,=,>) και περιγράφουμε τη στρατηγική που χρησιμοποιήσαμε σε κάθε περίπτωση.

Σύγκριση και διάταξη κλασμάτων

Ενότητα 3

Στρατηγικές σύγκρισης		Εξήγηση των στρατηγικών
Στα κλάσματα που έχουν ίσους παρονομαστές, μεγαλύτερο είναι το κλάσμα που έχει μεγαλύτερο αριθμητή.		$\dfrac{5}{7} > \dfrac{4}{7}$ Tα 5 είναι περισσότερα από τα 4 μέρη του ίδιου μεγέθους (έβδομα).
Στα κλάσματα που έχουν ίσους αριθμητές, μεγαλύτερο είναι το κλάσμα που έχει μικρότερο παρονομαστή.		$\dfrac{9}{5} > \dfrac{9}{6}$ Παίρνουμε ίδιο αριθμό από μέρη (9), αλλά τα πέμπτα είναι μεγαλύτερα σε μέγεθος μέρη από τα έκτα .
Ένα κλάσμα που έχει μεγαλύτερο αριθμητή και μικρότερο παρονομαστή από ένα άλλο κλάσμα είναι μεγαλύτερο από αυτό.		$\dfrac{18}{24} > \dfrac{16}{27}$ Παίρνουμε και περισσότερα μέρη (18) και μεγαλύτερου μεγέθους, αφού τα εικοστά τέταρτα είναι μεγαλύτερα από τα εικοστά έβδομα.
Μπορούμε να συγκρίνουμε κλάσματα χρησιμοποιώντας ένα κοινό σημείο αναφοράς.		$\dfrac{12}{13} > \dfrac{8}{9}$ Tα δύο κλάσματα είναι μικρότερα από το 1. Το $\dfrac{12}{13}$ βρίσκεται πιο κοντά στο 1, γιατί απέχει $\dfrac{1}{13}$ , το οποίο είναι λιγότερο από το $\dfrac{1}{9}$ που απέχει το $\dfrac{8}{9}$ .

Εφαρμογή

Να συγκρίνετε τα κλάσματα $\dfrac{3}{7}$ και $\dfrac{5}{8}$ .

α΄ τρόπος:Μετατρέπουμε σε ισοδύναμα κλάσματα που έχουν ίδιο παρονομαστή.

Βρίσκουμε το Ε.Κ.Π των παρονομαστών: Ε.Κ.Π. (7,8) = ……...………………………
Δημιουργούμε κλάσματα ισοδύναμα με τα αρχικά με παρονομαστή ίδιο με το Ε.Κ.Π. (7,8).
Έχουμε: $\dfrac{3}{7}= \dfrac{{3} \text{☓} {◻}}{{7} \text{☓} {◻}}=\dfrac{◻}{◻}$ και $\dfrac{5}{8} = \dfrac{{5} \text{☓} {◻}}{{8} \text{☓} {◻}}=\dfrac{◻}{◻}$ .
Συγκρίνουμε τους αριθμητές των δύο νέων κλασμάτων, άρα $\dfrac{◻}{◻} \dfrac{◻}{◻}$ .

β΄ τρόπος:Συγκρίνουμε ως προς ένα κοινό σημείο αναφοράς.

Επιλέγουμε το $\dfrac{1}{2}$ ως σημείο αναφοράς, για να συγκρίνουμε τα δύο κλάσματα.
Συγκρίνουμε το $\dfrac{5}{8}$ με το $\dfrac{1}{2}$ . Το $\dfrac{1}{2}$ είναι ισοδύναμο με το $\dfrac{4}{8}$ .Είναι $\dfrac{5}{8}$ > $\dfrac{4}{8}$ , άρα $\dfrac{5}{8}$ $\dfrac{1}{2}$ .
Συγκρίνουμε το $\dfrac{3}{7}$ με το $\dfrac{1}{2}$ . Το $\dfrac{1}{2}$ είναι ισοδύναμο με το $\dfrac{3}{6}$ . Είναι $\dfrac{3}{7}$ < $\dfrac{3}{6}$ , άρα $\dfrac{3}{7}$ $\dfrac{1}{2}$ .
Επομένως , έχουμε τελικά: $\dfrac{◻}{◻} \dfrac{◻}{◻}$ .

Αναστοχασμός

Βρίσκουμε κλάσματα που είναι μικρότερα από το $\dfrac{1}{2}$ .
Τα κλάσματα $\dfrac{13}{15}$ και $\dfrac{17}{19}$ είναι ισοδύναμα ή όχι; Αιτιολογούμε την απάντησή μας.
Βρίσκουμε κλάσματα όσο γίνεται πιο κοντά στο 1.