Μαθηματικά (Ε' Δημοτικού) - Βιβλίο Μαθητή (Εμπλουτισμένο)
1. Οι μαθητές και οι μαθήτριες της Ε΄ τάξης κάνουν συλλογή από γραμματόσημα. Παρατηρούμε την παρακάτω σελίδα.
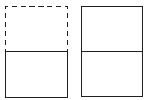
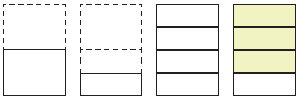
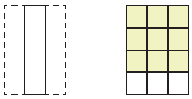
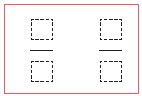
Τα δυο κλάσματα εκφράζουν το ……..... μέρος της σελίδας.
Πώς προκύπτουν οι όροι του κλάσματος $\dfrac{9}{12}$ από τους όρους του κλάσματος $\dfrac{3}{4}$ ;
………………………………………………………………………………………………………………
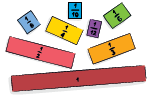
2. Εκφράζουμε το κλάσμα $\dfrac{6}{12}$ με κλάσματα που έχουν μικρότερους όρους χρησιμοποιώντας τις ράβδους κλασμάτων του παραρτήματος.
$\dfrac{6}{12}$ = $\dfrac{}{6}$ = $\dfrac{}{4}$ = $\dfrac{}{2}$
Πώς προκύπτουν οι όροι των κλασμάτων που βρήκαμε από τους όρους του $\dfrac{6}{12}$;
...........................................................................................................................................................
...........................................................................................................................................................
...........................................................................................................................................................
Ποιο κλάσμα έχει τους μικρότερους όρους;.......................................................................................
| Βασικές μαθηματικές έννοιες και διεργασίες |
|
Παραδείγματα |
| Τα κλάσματα που εκφράζουν το ίδιο μέρος ενός όλου λέγονται ισοδύναμα ή ίσα. |
|
$\dfrac{1}{3}=\dfrac{4}{12}$ |
| Αν πολλαπλασιάσουμε τον αριθμητή και τον παρονομαστή ενός κλάσματος με τον ίδιο αριθμό, προκύπτει κλάσμα ισοδύναμο με το αρχικό. |
|
$\dfrac{3}{4}=\dfrac{{3} \text{☓} {\color{#F05A67}2}}{{4} \text{☓} {\color{#F05A67}2}}=\dfrac{6}{8}$ |
| Αν διαιρέσουμε τον αριθμητή και τον παρονομαστή ενός κλάσματος με τον ίδιο αριθμό, προκύπτει κλάσμα ισοδύναμο με το αρχικό, με μικρότερους όρους. Η διαδικασία αυτή λέγεται απλοποίηση. |
|
$\dfrac{16}{24}=\dfrac{{16} \text{∶} {\color{#F05A67}8}}{{24}\text{∶}{8}}=\dfrac{2}{3}$ |
| Τα κλάσματα που οι όροι τους δεν απλοποιούνται λέγονται ανάγωγα. |
|
$\dfrac{3}{4}$, $\dfrac{5}{7}$, $\dfrac{1}{8}$ |
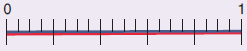
1. Ο λαγός και η χελώνα τρέχουν την ίδια διαδρομή. Ο λαγός έχει διανύσει τα $\dfrac{8}{20}$ της διαδρομής και η χελώνα τα $\dfrac{2}{5}$ της. Να τοποθετήσετε τα δύο κλάσματα πάνω στην αριθμογραμμή. Τι παρατηρείτε;
Τοποθετούμε τα κλάσματα στην αριθμογραμμή, την οποία χωρίζουμε κάθε φορά κατάλληλα.
Παρατηρούμε ότι τα κλάσματα βρίσκονται στο …………………
σημείο της αριθμογραμμής.
Επαλήθευση: Απλοποιούμε το κλάσμα $\dfrac{8}{20}$, ώστε να γίνει ανάγωγο.
2. Να βρείτε ένα κλάσμα μεταξύ των κλασμάτων $\dfrac{1}{3}$ και $\dfrac{2}{3}$ .
Βρίσκουμε για καθένα από τα παραπάνω κλάσματα ένα ισοδύναμό του. $\dfrac{1}{3} = \dfrac{{1} \text{☓} {◻}}{{3} \text{☓} {◻}}=\dfrac{◻}{◻}$ και $\dfrac{2}{3} = \dfrac{{2} \text{☓} {◻}}{{3} \text{☓} {◻}}=\dfrac{◻}{◻}$
Ανάμεσα στα κλάσματα $\dfrac{◻}{◻}$ και $\dfrac{◻}{◻}$ που δημιουργήσαμε, βρίσκεται το κλάσμα $\dfrac{◻}{◻}$.
