Μαθηματικά (Ε' Δημοτικού) - Βιβλίο Μαθητή (Εμπλουτισμένο)

Το κλάσμα ως πηλίκο διαίρεσης

15

Εικόνα

Διερεύνηση

Εικόνα

Η γιαγιά θέλει να μοιράσει εξίσου μερικές σοκολάτες στα 4 εγγόνια της.

α. Αν οι σοκολάτες είναι 8, τι μέρος από αυτές θα πάρει το κάθε παιδί;
Γράφουμε την πράξη και υπολογίζουμε: ……………………………………


Εικόνα

Όταν μοιράζουμε, το αποτέλεσμα είναι πάντοτε φυσικός αριθμός;
Συζητάμε με τους συμμαθητές και τις συμμαθήτριές μας.

β. Αν οι σοκολάτες είναι 3, τι μέρος από αυτές θα πάρει το κάθε παιδί;

Εικόνα

Εργαζόμαστε με τον τρόπο τον οποίο μας προτείνει ο Νίκος.

Κάθε παιδί θα πάρει
της σοκολάτας.

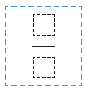
Εικόνα



Εικόνα

Παρατηρούμε το σχέδιο και συζητάμε τι δείχνουν οι όροι του κλάσματος.

Αριθμητής: .......................................................................................

Παρονομαστής:................................................................................    Άρα

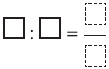
Εικόνα

...........................................................................................................

γ. Αν οι σοκολάτες είναι 5, τι μέρος από αυτές θα πάρει το κάθε παιδί;
Εργαζόμαστε σχεδιάζοντας και χωρίζοντας τις σοκολάτες

Κάθε παιδί θα πάρει
σοκολάτες.

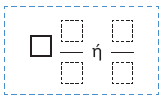
Εικόνα



Άρα

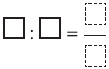
Εικόνα

Το κλάσμα ως πηλίκο διαίρεσης

Ενότητα 3

Βασικές μαθηματικές έννοιες και διεργασίες

 

 Παραδείγματα
Κάθε κλάσμα εκφράζει το πηλίκο της διαίρεσης του αριθμητή διά του παρονομαστή.

 

 $\dfrac{3}{4}$=3:4 , $\dfrac{24}{5}$ = 24:5
Κάθε φυσικός αριθμός μπορεί να γραφτεί με τη μορφή κλάσματος.

 

 5 = 5:1 = $\dfrac{5}{1}$ ή 5 = $\dfrac{5}{1}$ = $\dfrac{10}{2}$ = $\dfrac{15}{3}$ κλπ.

Στρατηγικές διαχείρισης αριθμών

1.  Μετατροπή ενός κλάσματος σε δεκαδικό αριθμό.
Μετατρέπουμε ένα κλάσμα σε δεκαδικό αριθμό διαιρώντας τον αριθμητή με τον παρονομαστή του.

    Π.χ. α. $\dfrac{3}{10}$=3:10=0,3      β. $\dfrac{3}{5}$=3:5=0,6      γ. $\dfrac{7}{9}$ = 7:9=0,777…      δ. $\dfrac{9}{2}$ = 9:2=4,5

Σημείωση: Χρησιμοποιούμε την αριθμομηχανή τσέπης, για να βρούμε το αποτέλεσμα.

2. Μετατροπή ενός κλάσματος μεγαλύτερου της μονάδας σε μεικτό αριθμό.

π.χ. Μετατρέπουμε το κλάσμα $\dfrac{36}{7}$ σε μεικτό αριθμό.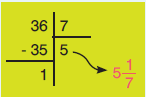

Εικόνα
  1. Διαιρούμε τον αριθμητή του κλάσματος με τον παρονομαστή, γιατί $\dfrac{36}{7}$ = 36:7.
  2. Ο ακέραιος του μεικτού αριθμού είναι το πηλίκο της διαίρεσης και δείχνει πόσες επτάδες χωράνε στο 36.
  3. Το κλάσμα του μεικτού έχει: α. αριθμητή το υπόλοιπο της διαίρεσης και

    β. παρονομαστή τον διαιρέτη.      Άρα $\dfrac{36}{7}$ = 5 $\dfrac{1}{7}$
Εικόνα

Εφαρμογή

Ο Νίκος και οι 4 φίλοι του μοιράστηκαν εξίσου 6 μήλα.
Τι μέρος από τα μήλα πήρε το κάθε παιδί;
Θέλουμε να μοιράσουμε τα 6 μήλα στα 5 παιδιά.
α΄ τρόπος:Χωρίζουμε κάθε μήλο σε 5 ίσα μέρη, όσα είναι τα παιδιά. Κάθε κομμάτι είναι το $\dfrac{1}{5}$ .
Κάθε παιδί θα πάρει 6 τέτοια κομμάτια, όσα είναι τα μήλα, δηλαδή 6 $\text{☓}$ $\dfrac{1}{5}$ = $\dfrac{6}{5}$ .
β΄ τρόπος:Θα κάνουμε διαίρεση 6 : 5 = $\dfrac{6}{5}$ . Κάθε παιδί πήρε τα $\dfrac{6}{5}$ ή 1 $\dfrac{1}{5}$ των μήλων.

Εικόνα

Αναστοχασμός

  1. Ο παρονομαστής ενός κλάσματος μπορεί να είναι μηδέν;
  2. Κάθε κλάσμα μπορεί να θεωρηθεί ως το αποτέλεσμα μιας διαίρεσης.
    Φτιάχνουμε ένα πρόβλημα διαίρεσης. Τι δείχνει ο αριθμητής και τι ο παρονομαστής;