Μαθηματικά (Ε' Δημοτικού) - Βιβλίο Μαθητή (Εμπλουτισμένο)
Η Δανάη, η Αγγελική και ο Αντρέι φτιάχνουν προσκλήσεις για τη γιορτή του σχολείου τους.
α΄ τρόπος: Σχεδιάζουμε τα κομμάτια από τα χαρτόνια που έχουν τα κορίτσια.
Γράφουμε κάτω από κάθε κομμάτι το κλάσμα που εκφράζει το μέρος του χαρτονιού.
Γράφουμε με κλάσμα το μέρος από το χαρτόνι που έχουν συνολικά τα κορίτσια: 
Παρατηρούμε ότι στο κλάσμα αυτό ο αριθμητής είναι ……………………………
από τον παρονομαστή.
β΄ τρόπος: Σχεδιάζουμε τα κομμάτια και γράφουμε με κλάσματα το χαρτόνι που έχουν τα κορίτσια, σχηματίζοντας:
τα ολόκληρα χαρτόνια
και
τα μέρη του χαρτονιού που έμειναν.
+
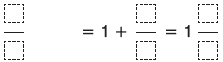
Παρατηρούμε ότι
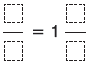
| Βασικές μαθηματικές έννοιες και διεργασίες |
|
Παραδείγματα |
| Τα κλάσματα στα οποία ο αριθμητής είναι μεγαλύτερος από τον παρονομαστή είναι μεγαλύτερα από τον αριθμό 1. |
|
$\dfrac{5}{3}$ > 1 |
| Τα κλάσματα αυτά μπορούμε να τα μετατρέψουμε σε μεικτούς αριθμούς γράφοντας χωριστά τις ακέραιες μονάδες τους. |
|
$\dfrac{5}{3}=\dfrac{3}{3}+\dfrac{2}{3}=1+\dfrac{2}{3}=1\dfrac{2}{3}$ (μεικτός) |
1. Να μετατρέψετε το κλάσμα $\dfrac{9}{4}$ σε μεικτό αριθμό.
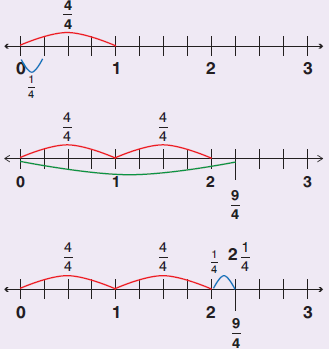
Άρα: $\dfrac{9}{4}=\text{—}+\text{—}+\text{—}=1+1+\dfrac{1}{4}=2+\dfrac{1}{4}=2 \dfrac{1}{4}$
2. Να μετατρέψετε τον μεικτό αριθμό 2$\dfrac{1}{4}$ σε κλάσμα.
Ο παρονομαστής δείχνει ότι χωρίζουμε την ακέραιη μονάδα σε ……… ίσα μέρη.
Η ακέραιη μονάδα είναι ίση με $\text{—}$.
Άρα: 2$\dfrac{1}{4}=2+\dfrac{1}{4}=1+1+\dfrac{1}{4}=\text{—}+\text{—}+\text{—}=\dfrac{9}{4}$
Αν το κλάσμα $\dfrac{α}{3}$ είναι μεγαλύτερο της ακέραιης μονάδας, ποιος αριθμός μπορεί να είναι το α;
Τι συμπεραίνουμε; . ……………………………………………………………..
