Οι κλασματικοί αριθμοί

13

Διερεύνηση

1. Τα παιδιά της τάξης ύστερα από επίσκεψή τους σε ένα μουσείο με έργα του Ολλανδού ζωγράφου Μοντριάν, δημιούργησαν τους δικούς τους πίνακες. Ένας από αυτούς είναι και ο παρακάτω.

Κόβουμε τα κομμάτια του πίνακα από το παράρτημα και με τη βοήθεια τους υπολογίζουμε.

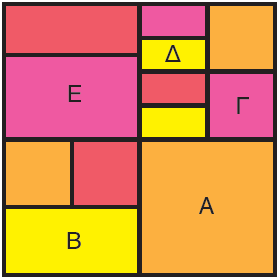
Γράφουμε με αριθμό το μέρος του πίνακα που καλύπτουν τα γεωμετρικά σχήματα:

Α =

Β =

Γ =

Δ =

Ε =

Συζητάμε τους διαφορετικούς τρόπους με τους οποίους μπορούμε να υπολογίσουμε το μέρος που καλύπτει το σχήμα Ε.

2. Η Δανάη διάλεξε τις χάντρες της εικόνας, για να φτιάξει ένα βραχιόλι.

Συζητάμε τους διαφορετικούς τρόπους με τους οποίους μπορούμε να εκφράσουμε το μέρος των κίτρινων και κόκκινων χαντρών.

Οι κλασματικοί αριθμοί

Ενότητα 3

Βασικές μαθηματικές έννοιες και διεργασίες		Παραδείγματα
Κάθε κλάσμα είναι ένας αριθμός. Σχηματίζεται από τον αριθμητή και τον παρονομαστή, που λέγονται όροι του κλάσματος και χωρίζονται με τη γραμμή κλάσματος.		Διαβάζουμε: τρία τέταρτα
Ένα κλάσμα μπορεί να εκφράζει μια ποσότητα από κάτι ολόκληρο, το μέρος ενός όλου. Το ολόκληρο ή όλο το λέμε ακέραιη μονάδα.		Τα ${}\dfrac{{{2}}}{5}$ από το σύνολο των γεωμετρικών σχημάτων είναι τρίγωνα.
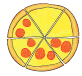
Όταν το κλάσμα δείχνει το μέρος ενός όλου τότε: ο παρονομαστής δείχνει σε πόσα ίσα μέρη χωρίζουμε το όλο. Ο αριθμητής δείχνει πόσα από αυτά τα ίσα μέρη παίρνουμε.		Μέρος του όλου Τα ${}\dfrac{{{4}}}{6}$ της πίτσας έχουν ντομάτα Παρονομαστής: 6, σε τόσα ίσα κομμάτια χωρίζουμε Αριθμητής: 4, τόσα κομμάτια έχουν ντομάτα
Όταν ο παρονομαστής είναι ίσος με τον αριθμητή, το κλάσμα είναι ίσο με την ακέραιη μονάδα.		$\dfrac{1}{1}=\dfrac{2}{2}=\dfrac{3}{3}=\dfrac{4}{4}...=\dfrac{15}{15}...=1$

Εφαρμογή Κλάσματα στην αριθμογραμμή

Να τοποθετήσετε πάνω στην αριθμογραμμή τα κλάσματα: $\dfrac{1}{4}$, $\dfrac{3}{4}$ και $\dfrac{4}{4}$

1o βήμα:Χωρίζουμε κάθε μονάδα στην αριθμογραμμή σε .........................................
......................................................................
.....................................................................................................................................................................

2ο βήμα:Προσδιορίζουμε πάνω στην αριθμογραμμή την κλασματική μονάδα $\dfrac{1}{4}$
3ο βήμα:Για να τοποθετήσουμε το κλάσμα $\dfrac{3}{4}$, επαναλαμβάνουμε 3 φορές την κλασματική μονάδα $\dfrac{1}{4}$. Προσδιορίζουμε πάνω στην αριθμογραμμή το κλάσμα $\dfrac{3}{4}$.
4ο βήμα: Προσδιορίζουμε πάνω στην αριθμογραμμή το κλάσμα $\dfrac{4}{4}$.
Παρατηρούμε ότι $\dfrac{4}{4}$= ……

Μικροπείραμα Μικροπείραμα Μικροπείραμα Μικροπείραμα

Αναστοχασμός

Γράφουμε με κλάσμα το μέρος των παιδιών της τάξης μας που έχουν ένα κοινό χαρακτηριστικό:
....................................................................................................................................................
Βρίσκουμε κλάσματα μικρότερα, ίσα και μεγαλύτερα της μονάδας.
Δημιουργούμε μία έντυπη ή ψηφιακή αφίσα και καταγράφουμε σε αυτήν τρεις εκφράσεις από την καθημερινή μας ζωή στις οποίες χρησιμοποιούμε κλάσματα. Σχεδιάζουμε εικόνες, για να αναπαραστήσουμε τα κλάσματα αυτά.