Η διαίρεση στους φυσικούς αριθμούς

12

Διερεύνηση

1. Ένας χώρος στάθμευσης έχει 21 σειρές, καθεμιά από τις οποίες έχει 8 θέσεις.
Πόσες θέσεις έχει συνολικά ο χώρος στάθμευσης;
Λύνουμε το παραπάνω πρόβλημα και, με βάση αυτό, διατυπώνουμε προβλήματα διαίρεσης.

Λύση

.......................................................................................................................................................

Πρόβλημα

.......................................................................................................................................................

Συζητάμε πόσα προβλήματα διαίρεσης μπορούμε να διατυπώσουμε με βάση το παραπάνω πρόβλημα.

Σε τι μοιάζουν αυτά τα προβλήματα;
Σε τι διαφέρουν αυτά τα προβλήματα;

2. Σε πόσες σειρές του παραπάνω χώρου σταθμεύουν 152 αυτοκίνητα;
Σε πόσες σειρές του σταθμεύουν 156 αυτοκίνητα;

Συζητάμε τους τρόπους με τους οποίους μπορούμε να δείξουμε το πηλίκο καθεμιάς από τις παραπάνω διαιρέσεις με τη βοήθεια:

τετραγωνισμένου χαρτιού
υλικού δεκαδικής βάσης

Η διαίρεση στους φυσικούς αριθμούς

Ενότητα 2

Βασικές μαθηματικές έννοιες και διεργασίες		Παραδείγματα
Όταν έχουμε δύο φυσικούς αριθμούς Δ και δ, τότε μπορούμε να βρούμε δύο άλλους μοναδικούς φυσικούς αριθμούς π και υ, έτσι ώστε να ισχύει: Δ = δ x π + υ. Ο αριθμός Δ ονομάζεται Διαιρετέος, ο δ διαιρέτης, ο π πηλίκο και ο υ υπόλοιπο της διαίρεσης. Το υπόλοιπο είναι πάντα αριθμός μικρότερος από τον διαιρέτη και μεγαλύτερος ή ίσος του μηδενός.
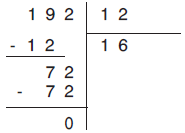
Αν το υπόλοιπο υ είναι 0, τότε έχουμε μία Τέλεια Διαίρεση: Δ = δ x π
Η διαίρεση της μορφής Δ = δ x π + υ λέγεται Ευκλείδεια Διαίρεση.

Εφαρμογή

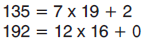
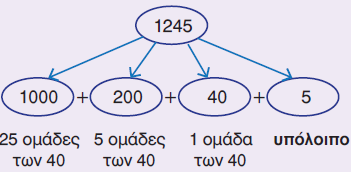
Να υπολογίσετε το πηλίκο της διαίρεσης 1.245:40.

Μπορούμε να αναλύσουμε τον αριθμό,
όπως φαίνεται στο διπλανό σχήμα:

1.245 = 40 x (... + ... + ...) + 5 = 40 x ... + 5

Το πηλίκο της διαίρεσης 1.245:40 είναι ... και η διαίρεση είναι ατελής.

Αναστοχασμός

Προτείνουμε έναν τρόπο επαλήθευσης της διαίρεσης: 249 : 20.
Ποιο είναι το πηλίκο μιας διαίρεσης, όταν ο Διαιρετέος είναι ίσος με τον διαιρέτη;
Ποιο είναι το πηλίκο μιας διαίρεσης, όταν ο διαιρέτης είναι ο αριθμός 1;
Ποιο είναι το πηλίκο μιας διαίρεσης, όταν ο Διαιρετέος είναι 0;
Ανφέρουμε ένα παράδειγμα που να δείχνει ότι η τέλεια διαίρεση είναι αντίστροφη πράξη του πολλαπλασιασμού.