Ηλεκτρικά δίπολα και αντίσταση ενός αγωγού
Συμπλήρωσε τις λέξεις που λείπουν από το παρακάτω κείμενο έτσι ώστε οι προτάσεις που προκύπτουν να είναι επιστημονικά ορθές:
α. Ηλεκτρική ............... (R) ενός ηλεκτρικού διπόλου ονομάζεται το πηλίκο της .............................. (V) που εφαρμόζεται στους πόλους του διπόλου προς την ............ (Ι) του .............................. που το διαρρέει: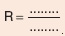 Η μονάδα αντίστασης στο Διεθνές Σύστημα Μονάδων είναι το ......... (1 .....). Η μονάδα αντίστασης στο Διεθνές Σύστημα Μονάδων είναι το ......... (1 .....).
β. Η αντίσταση του μεταλλικού αγωγού προέρχεται από τις ............... των ελεύθερων ηλεκτρονίων με τα ............... του μετάλλου.
γ. Η ένταση (I) του ηλεκτρικού ρεύματος που διαρρέει ένα μεταλλικό αγωγό είναι ............... της διαφοράς δυναμικού (V) που εφαρμόζεται στα άκρα του με σταθερά αναλογίας το 
δ. Κάθε δίπολο που ικανοποιεί το νόμο του Ωμ ονομάζεται ............... και έχει την ιδιότητα να μετατρέπει εξ ολοκλήρου την ............... ενέργεια σε ................
ε. Η αντίσταση ενός μεταλλικού σύρματος σταθερής διατομής σε όλο το μήκος του: i) είναι ............... του ............... του (,), ....................... του εμβαδού (Α) της διατομής του, ii) εξαρτάται από το ............. του ........... από το οποίο είναι κατασκευασμένο το σύρμα και από τη ............... του αγωγού.
στ. Όταν ο μεταβλητός αντιστάτης χρησιμοποιείται για να ρυθμίζουμε την ένταση του ηλεκτρικού ρεύματος που διαρρέει μια συσκευή ονομάζεται ...................., ενώ για να ρυθμίζουμε την ηλεκτρική τάση που εφαρμόζεται στους πόλους της ονομάζεται ........................
Εφαρμογές αρχών διατήρησης στη μελέτη απλών ηλεκτρικών κυκλωμάτων
Συμπλήρωσε τις λέξεις που λείπουν από το παρακάτω κείμενο έτσι ώστε οι προτάσεις που προκύπτουν να είναι επιστημονικά ορθές:
α. Η τάση VΑΓ στα άκρα του κυκλώματος δύο λαμπτήρων συνδεδεμένων σε σειρά ισούται με το ................. των τάσεων VΑΒ και VΒΓ στα άκρα κάθε λαμπτήρα. Αυτό είναι αποτέλεσμα της αρχής ............................. της .......................
β. Η ένταση (I) του ολικού ηλεκτρικού ρεύματος που διαρρέει ένα κύκλωμα δύο λαμπτήρων συνδεδεμένων παράλληλα είναι ίση με το .................. των ............... (I1 και I2) των .................... που διαρρέουν τους δύο λαμπτήρες. Αυτό είναι αποτέλεσμα της αρχής ............... του .....................................
Εφάρμοσε τις γνώσεις σου και γράψε τεκμηριωμένες απαντήσεις στις ερωτήσεις που ακολουθούν:
Ηλεκτρικό ρεύμα και ηλεκτρικό κύκλωμα
| Να πραγματοποιήσεις το κύκλωμα που παριστάνεται στη διπλανή εικόνα. Ζωγράφισε στο τετράδιό σου τη σχηματική του αναπαράσταση. Να περιγράψεις τι θα συμβεί μετά το κλείσιμο του διακόπτη χρησιμοποιώντας τις έννοιες «ηλεκτρική τάση», «ηλεκτρικό ρεύμα», «ηλεκτρικό κύκλωμα», «ηλεκτρικό πεδίο», «ελεύθερα ηλεκτρόνια». |
 |
Διαθέτεις μια μπαταρία, ένα λαμπτήρα, ένα αμπερόμετρο, ένα βολτόμετρο, ένα διακόπτη και καλώδια. Πραγματοποίησε ένα κύκλωμα τέτοιο ώστε όταν κλείνεις το διακόπτη, ο λαμπτήρας να φωτοβολεί, ενώ το αμπερόμετρο να δείχνει την ένταση του ηλεκτρικού ρεύματος που διαρρέει το λαμπτήρα και το βολτόμετρο την ηλεκτρική τάση στα άκρα του. Να σχεδιάσεις τη σχηματική αναπαράσταση του παραπάνω κυκλώματος καθώς και τη συμβατική φορά του ρεύματος. |