Μαθηματικά Γ΄ Γυμνασίου - Βιβλίο Μαθητή (εμπλουτισμένο)
2.3
Σχέσεις μεταξύ τριγωνομετρικών αριθμών μιας γωνίας
Εικόνα
Εικόνα
  • Γνωρίζω ποιες είναι οι βασικές τριγωνομετρικές ταυτότητες και πως αποδεικνύονται.
  • Τις χρησιμοποιώ τις βασικές τριγωνομετρικές ταυτότητες για την απόδειξη απλών τριγωνομετρικών ταυτοτήτων.
ΔΡΑΣΤΗΡΙΟΤΗΤΑ

Σε ορθοκανονικό σύστημα να πάρετε ένα σημείο Μ στο 1ο ή στο 2ο τεταρτημόριο με όποιες συντεταγμένες θέλετε.

1. Να υπολογίσετε τους τριγωνομετρικούς αριθμούς της γωνίας ω = xÔM.

2. Να υπολογίσετε την παράσταση (ημω)2 + (συνω)2 και να συγκρίνετε το αποτέλεσμα που βρήκατε με τα αποτελέσματα που βρήκαν οι συμμαθητές σας.

3. Να υπολογίσετε το λόγοεικόνα και να τον συγκρίνετε με την εφω.

εικόνα

Μικροπείραμα μικροπείραμα    Μικροπείραμα μικροπείραμα
ΠΑΡΑΔΕΙΓΜΑΤΑ − ΕΦΑΡΜΟΓΕΣ
1

Αν για την αμβλεία γωνία ω ισχύει ημω = 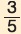εικόνα , τότε να υπολογιστούν οι άλλοι τριγωνομετρικοί αριθμοί της γωνίας ω.

 

Λύση

Από την ταυτότητα ημ2ω + συν2ω = 1 έχουμε

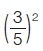
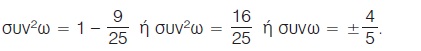
συν2ω = 1 - ημ2ω ή συν2ω = 1 - εικόνα

εικόνα

Επειδή η γωνία ω είναι αμβλεία έχουμε συνω < 0, οπότε συνω = 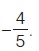εικόνα

Από την ταυτότητα 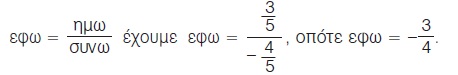εικόνα

2

Αν για την οξεία γωνία ω ισχύει εφω = 2, τότε να υπολογιστούν οι άλλοι τριγωνομετρικοί αριθμοί της γωνίας ω.

 

Λύση

εικόνα

3

Να αποδειχθούν οι ταυτότητες:

α) (ημx - συνx)2 + 2ημxσυνx = 1 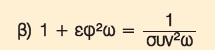εικόνα

 

Λύση

α) Έχουμε

(ημx- συνx)2 + 2ημxσυνx = ημ2x - 2ημxσυνx + συν2x + 2ημxσυνx = ημ2x + συν2x = 1

β) Έχουμε

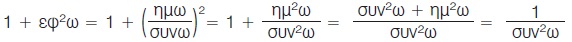
εικόνα
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ
1

Να χαρακτηρίσετε τις παρακάτω ισότητες με (Σ), αν είναι σωστές ή με (Λ), αν είναι λανθασμένες:

α)εικόνα Εικόνα
β) Αν συνω = 0, τότε δεν ορίζεται η εφω. Εικόνα
γ) Για κάθε γωνία ω ισχύει ημ2ω = συν2ω - 1. Εικόνα
δ) εικόνα Εικόνα
2

O Στέφανος ισχυρίζεται ότι δεν υπάρχει γωνία ω, τέτοια ώστε ημω = 0 και συνω = 0. Έχει δίκιο; Να αιτιολογήσετε την απάντηση σας.

Μικροπείραμα μικροπείραμα

3

Να συμπληρώσετε τα κενά στις παρακάτω προτάσεις:

α) Αν ημω = 1, τότε συνω = .............

β) Αν ημω = 0, τότε συνω = .............

4

εικόνα

ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ − ΠΡΟΒΛΗΜΑΤΑ

1

Αν για την οξεία γωνία ω ισχύει ημω =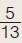εικόνα , τότε να υπολογίσετε τους άλλους τριγωνομετρικούς αριθμούς της γωνίας ω.

 

2

Αν για την αμβλεία γωνία ω ισχύει συνω =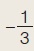εικόνα , τότε να υπολογίσετε τους άλλους τριγωνομετρικούς αριθμούς της γωνίας ω.

3

Αν για την οξεία γωνία ω ισχύει εφω =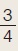εικόνα , τότε να υπολογίσετε τους άλλους τριγωνομετρικούς αριθμούς της γωνίας ω.

Μικροπείραμα μικροπείραμα

4

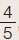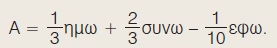
Αν για την αμβλεία γωνία ω ισχύει ημω =εικόνα , τότε να υπολογίσετε την παράσταση:

εικόνα

5

Να αποδείξετε ότι:

α) ημ3ω + ημωσυν2ω = ημω

β) συν2ω - συν4ω = ημ2ωσυν2ω ;

6

Αν είναι x = 3συνω και y = 3ημω, τότε να αποδείξετε ότι:

α) xσυνω + yημω = 3

β) x2 + y2 = 9

7

Να αποδείξετε ότι:

α) συν2α - ημ2α = 2συν2α - 1

β) ημ2ασυν2β + ημ2αημ2β + συν2α = 1

8

Να αποδείξετε ότι:

α) (ημω + συνω)2 + (ημω - συνω)2 = 2

β) (αημω + βσυνω)2 + (βημω - ασυνω)2 = α2 + β2

9

Να αποδείξετε ότι:

εικόνα
10

Να αποδείξετε ότι:

εικόνα
11

Να υπολογίσετε τις παραστάσεις:

α) ημ50ºημ130º - συν50ºσυν130º

β) ημ214º + ημ2114º + συν2166º + συν266º

12

Να αποδείξετε ότι:

α) εφ70º συν70º - εφ110º συν110º = 0

β) εφ240º συν240º + συν2140º = 1

13

Αν είναι α = 30º και β = 60º, τότε να αποδείξετε ότι:

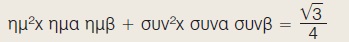
εικόνα

 

εικόνα

14
εικόνα

Είναι γωνία, όχι οξεία, ημίτονο έχει τον αριθμό 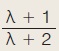εικόνακαι συνημίτονο έχει τον αριθμόεικόνα.

Ποια γωνία είναι;