- Γνωρίζω τους νόμους ημιτόνων και συνημιτόνων και μαθαίνω να τους εφαρμόζω στη λύση προβλημάτων.
Στην προηγούμενη τάξη μάθαμε να υπολογίζουμε τις πλευρές και τις γωνίες ενός ορθογωνίου τριγώνου, όταν γνωρίζουμε δύο πλευρές του ή μια πλευρά και μια οξεία γωνία του. Πώς όμως μπορούμε να υπολογίσουμε τις πλευρές και τις γωνίες ενός τριγώνου όταν δεν είναι ορθογώνιο;
Σχεδιάζουμε ένα οξυγώνιο τρίγωνο ΑΒΓ και φέρουμε το ύψος ΓΔ. Από τα ορθογώνια τρίγωνα ΑΔΓ και ΓΔΒ έχουμε:
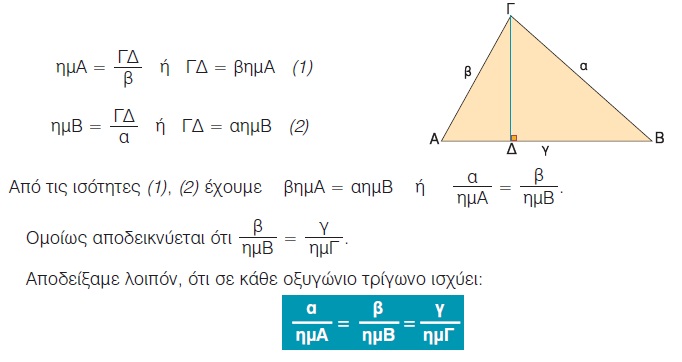
Η προηγούμενη σχέση αποδεικνύεται ότι ισχύει και όταν το τρίγωνο ΑΒΓ είναι αμβλυγώνιο ή ορθογώνιο και ονομάζεται νόμος των ημιτόνων.
Μικροπείραμα 
Γενικά
Οι πλευρές κάθε τριγώνου είναι ανάλογες προς τα ημίτονα των απέναντι γωνιών του.
Με το νόμο των ημιτόνων, αν γνωρίζουμε μια πλευρά ενός τριγώνου, την απέναντι γωνία της και μια άλλη πλευρά ή γωνία του, τότε μπορούμε να υπολογίσουμε τα υπόλοιπα πρωτεύοντα στοιχεία του (πλευρές - γωνίες).
Για παράδειγμα, στο τρίγωνο του διπλανού σχήματος μπορούμε με το νόμο των ημιτόνων να υπολογίσουμε τη γωνία 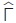 , αφού , αφού
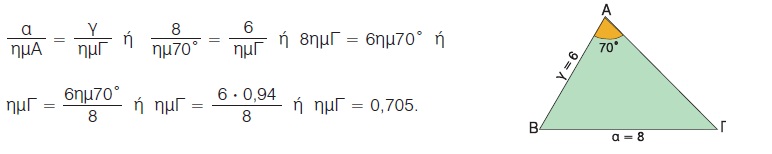
Από τους τριγωνομετρικούς πίνακες διαπιστώνουμε ότι 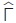 = 45º. = 45º.
Σ´ένα τρίγωνο ΑΒΓ, αν γνωρίζουμε τις τρεις πλευρές του ή δύο πλευρές και την περιεχόμενη γωνία τους, τότε με το νόμο των ημιτόνων δεν μπορούμε να υπολογίσουμε τα υπόλοιπα στοιχεία του τριγώνου, αφού δε γνωρίζουμε μια πλευρά και την απέναντι γωνία της.
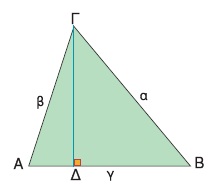
Αν το τρίγωνο είναι οξυγώνιο και φέρουμε το ύψος ΓΔ, τότε από το Πυθαγόρειο θεώρημα στο ορθογώνιο τρίγωνο ΔΒΓ έχουμε: α2 = ΔΓ2 + ΔΒ2 (1).
Επειδή ΔΒ = γ - ΑΔ, η ισότητα (1) γράφεται:
α2 = ΔΓ2 + (γ - ΑΔ)2 ή α2 = ΔΓ2 + γ2 + ΑΔ2 - 2γ·ΑΔ (2).
Από το ορθογώνιο τρίγωνο ΑΔΓ έχουμε: ΔΓ2 + ΑΔ2 = β2 και συνΑ =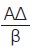 ή ΑΔ = βσυνΑ. ή ΑΔ = βσυνΑ.
Άρα η ισότητα (2) γράφεται: α2 = β2 + γ2 - 2βγσυνΑ
Η προηγούμενη σχέση αποδεικνύεται ότι ισχύει και όταν το τρίγωνο ΑΒΓ είναι αμβλυγώνιο ή ορθογώνιο και ονομάζεται νόμος των συνημιτόνων. Ομοίως αποδεικνύεται ότι σε κάθε τρίγωνο ΑΒΓ ισχύουν
β2 = γ2 + α2 - 2γασυνΒ
γ2 = α2 + β2 - 2αβσυνΓ
Με το νόμο των συνημιτόνων, αν σ' ένα τρίγωνο γνωρίζουμε τις τρεις πλευρές του ή δύο πλευρές και την περιεχόμενη γωνία τους, τότε μπορούμε να υπολογίσουμε τα υπόλοιπα πρωτεύοντα στοιχεία του.
Για παράδειγμα, αν στο τρίγωνο ΑΒΓ είναι α = 9 cm, β = 7 cm και γ = 6 cm, τότε μπορούμε να υπολογίσουμε τις γωνίες του.
Π.χ. για να υπολογίσουμε τη γωνία Β έχουμε:
β2 = γ2 + α2 - 2γασυνΒ ή
72 = 62 + 92 - 2 · 6 · 9 · συνΒ ή
49 = 36 + 81 - 108 · συνΒ ή 108 συνΒ = 68 ή
συνΒ = 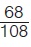 = 0,629. Από τους τριγωνομετρικούς πίνακες διαπιστώνουμε ότι = 0,629. Από τους τριγωνομετρικούς πίνακες διαπιστώνουμε ότι 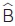 = 51º. = 51º. |
1
Σε τρίγωνο ΑΒΓ είναι 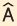 = 120º, = 120º, 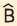 = 45º και α = 30 cm. Να υπολογιστεί η γωνία = 45º και α = 30 cm. Να υπολογιστεί η γωνία 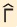 και η πλευρά β. και η πλευρά β.
Λύση
2
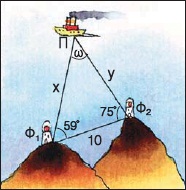
Δύο φάροι Φ1, Φ2 απέχουν μεταξύ τους 10 μίλια. Ένα πλοίο Π βρίσκεται σε μια θέση, όπως φαίνεται στο σχήμα. Να υπολογιστούν οι αποστάσεις x, y του πλοίου από κάθε φάρο.
Μικροπείραμα 
Λύση
Λύση
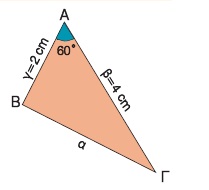
Από το νόμο των συνημιτόνων έχουμε:
α2 = β2 + γ2 - 2βγσυνΑ ή α2 = 42 + 22 - 2·4·2·συν60º
ή α2 = 16 + 4 - 16· ή α2 = 12.
Άρα α = √12 δηλαδή α = 2 √3 cm.
Ομοίως έχουμε:
β2 = γ2 + α2 - 2γασυνΒ ή 42 = 22 + ( 2 √3 )2 - 2· 2 √3 ·2·συνΒ ή
16 = 4 + 12 - 8√3 ·συνΒ ή 8√3 ·συνΒ = 0 ή συνΒ = 0, οπότε 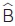 Β = 90º. Β = 90º.
Αφού 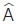 + +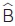 + + 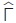 = 180º και = 180º και 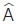 = 60º, = 60º, 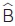 = 90º, έχουμε = 90º, έχουμε 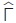 = 30º. = 30º.
1
Δύο δυνάμεις F1 = 4 Ν και F2 = 3 Ν εφαρμόζονται σ' ένα υλικό σημείο Ο και σχηματίζουν γωνία ω = 60º. Να υπολογιστεί η συνισταμένη τους F.
Λύση
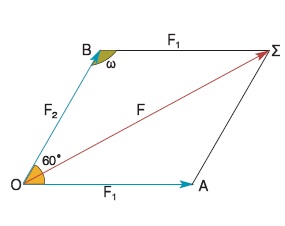
H συνισταμένη F των δυνάμεων F1, F2, όπως φαίνεται στο σχήμα, είναι η διαγώνιος του παραλληλογράμμου ΟΑΣΒ. Από το νόμο των συνημιτόνων στο τρίγωνο ΟΒΣ και επειδή ΒΣ = F1, έχουμε:
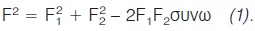
Οι γωνίες όμως ω και 60º είναι παραπληρωματικές, οπότε συνω = -συν60º και ο τύπος (1) γράφεται:
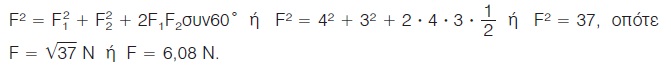
|
1
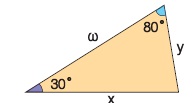
Να γράψετε τον νόμο των ημιτόνων στο τρίγωνο του διπλανού σχήματος ____ = ____ =____
2
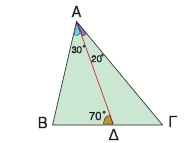
Να γράψετε τον νόμο των ημιτόνων:
α) στο τρίγωνο ΑΒΔ
____ = ____ = ____
β) στο τρίγωνο ΑΔΓ
____ = ____ = ____
3
Να χαρακτηρίσετε τις παρακάτω ισότητες με (Σ), αν είναι σωστές ή με (Λ), αν είναι λανθασμένες:

4
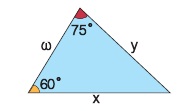
Να συμπληρώσετε τις παρακάτω ισότητες σύμφωνα με το νόμο των συνημιτόνων:
x2 = ……………………
y2 = ……………………
ω2 = ……………………
5
Να συμπληρώσετε τις παρακάτω προτάσεις
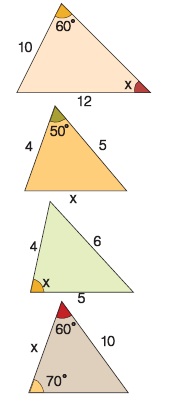
α) Η γωνία x υπολογίζεται με το νόμο των …………………… από την ισότητα ……………………
β) Η πλευρά x υπολογίζεται με το νόμο των …………………… από την ισότητα ……………………
γ) Η γωνία x υπολογίζεται με το νόμο των …………………… από την ισότητα ……………………
δ) Η πλευρά x υπολογίζεται με το νόμο των …………………… από την ισότητα ……………………
|
1
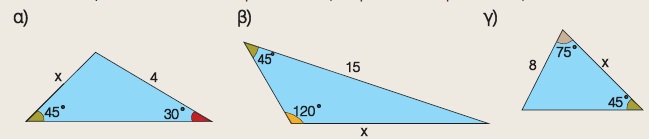
Να υπολογίσετε το x σε καθεμιά από τις παρακάτω περιπτώσεις:
2
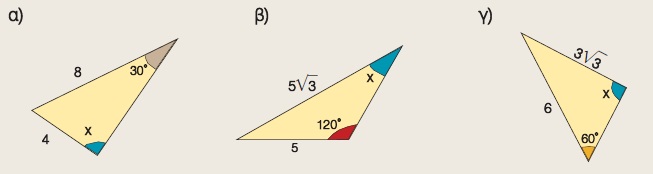
Να υπολογίσετε το x σε καθεμιά από τις παρακάτω περιπτώσεις:
3
Να υπολογίσετε τις υπόλοιπες γωνίες του τριγώνου ΑΒΓ, όταν:
α) α = 2, β = √2 και Β = 30º
β) β = √2 , γ = √3 και Γ = 60º.
4
Αν σε τρίγωνο ΑΒΓ είναι 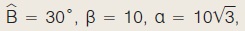 τότε να αποδείξετε ότι το τρίγωνο είναι ορθογώνιο ή ισοσκελές. τότε να αποδείξετε ότι το τρίγωνο είναι ορθογώνιο ή ισοσκελές.
5
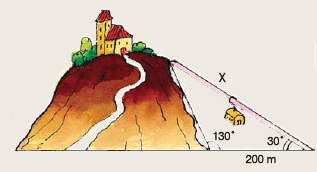
Να υπολογίσετε το μήκος της διαδρομής x του εναέριου σιδηροδρόμου στο διπλανό σχήμα. (Να χρησιμοποιήσετε τριγωνομετρικούς πίνακες).
6
Ένας μαθητής απευθυνόμενος στον καθηγητή του των Μαθηματικών είπε:
- Κύριε, σε ένα βιβλίο βρήκα μια άσκηση στην οποία έδινε ένα τρίγωνο ΑΒΓ με α = 12, β = 6, 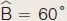 και ζητούσε να βρεθούν τα υπόλοιπα στοιχεία του. και ζητούσε να βρεθούν τα υπόλοιπα στοιχεία του.
Πώς λύνεται;
Ο καθηγητής αφού είδε την άσκηση τού είπε:
- Κάποιο λάθος έχεις κάνει, γιατί δεν υπάρχει τέτοιο τρίγωνο.
Πώς το κατάλαβε ο καθηγητής;
7
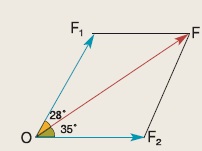
Οι δυνάμεις F1, F2 έχουν συνισταμένη F = 10 N που σχηματίζει με την F1 γωνία 28º και με την F2 γωνία 35º. Να υπολογίσετε τις δυνάμεις F1, F2. (Να χρησιμοποιήσετε τριγωνομετρικούς πίνακες).
9
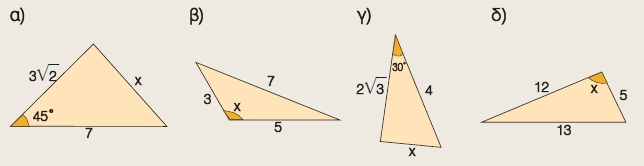
Να υπολογίσετε το x σε καθεμιά από τις παρακάτω περιπτώσεις:
10
Να υπολογίσετε τις ίσες πλευρές β, γ ισοσκελούς τριγώνου ΑΒΓ, αν 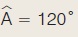 και α = 3√3 . και α = 3√3 .
11
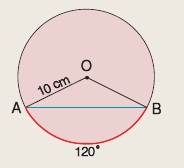
Σε κύκλο με ακτίνα R = 10 cm, η χορδή ΑΒ αντιστοιχεί σε τόξο 120º. Να υπολογίσετε το μήκος της χορδής.
12
Να υπολογίσετε τις διαγωνίους παραλληλογράμμου ΑΒΓΔ με ΑΒ = 4, ΒΓ = 3 και 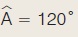
13
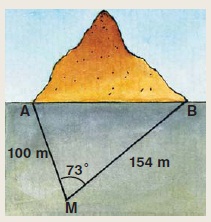
Μια τεχνική εταιρεία θέλει να καταθέσει μια προσφορά για την κατασκευή μιας σήραγγας ΑΒ. Ένας μηχανικός της εταιρείας με τους συνεργάτες του έστησε ένα γωνιόμετρο στη θέση Μ που η απόστασή του από το Α ήταν 100 m και από το Β ήταν 154 m. Αφού μέτρησε τη γωνία 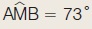 , ισχυρίστηκε ότι με αυτά τα στοιχεία μπορούσε να υπολογίσει το μήκος της σήραγγας. Είχε δίκιο ή άδικο; Πόσο ήταν τελικά το μήκος της σήραγγας; (Να χρησιμοποιήσετε τριγωνομετρικούς πίνακες). , ισχυρίστηκε ότι με αυτά τα στοιχεία μπορούσε να υπολογίσει το μήκος της σήραγγας. Είχε δίκιο ή άδικο; Πόσο ήταν τελικά το μήκος της σήραγγας; (Να χρησιμοποιήσετε τριγωνομετρικούς πίνακες).
Μικροπείραμα 
14
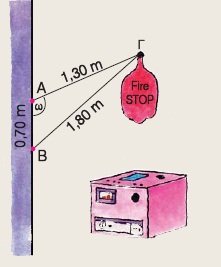
Ένας πυροσβεστήρας αυτόματης κατάσβεσης πρόκειται να στηριχτεί πάνω από τον καυστήρα ενός καλοριφέρ. Ένας τεχνικός θέλει να κατασκευάσει τη βάση στήριξης του και διαθέτει τρεις μεταλλικές βέργες ΑΒ = 0,70 m, ΑΓ = 1,30 m και ΒΓ = 1,80 m. Για να κολλήσει όμως κατάλληλα τις βέργες ΑΒ, ΑΓ, όπως φαίνεται στο σχήμα, πρέπει να γνωρίζει τη γωνία ω. Μπορείτε εσείς να την υπολογίσετε, ώστε να βοηθήσετε τον τεχνικό; (Να χρησιμοποιήσετε τριγωνομετρικούς πίνακες).

|
1
Να αποδείξετε ότι:
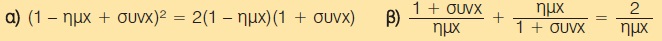
2
Σε ορθοκανονικό σύστημα αξόνων Οxy δίνεται το σημείο Α(4, 0) και το σημείο Μ που έχει τετμημένη –5, τεταγμένη θετική και η απόστασή του από το Ο είναι 13. Αν ω είναι η γωνία Α$\hat{O}$Μ, να υπολογίσετε το συνω και την απόσταση ΑΜ.
3
Σε τρίγωνο ΑΒΓ είναι ΒΓ = 30 cm, $\hat{B}$ = 45o και $\hat{Γ}$ = 75o . Να χαράξετε τη διχοτόμο ΑΔ του τριγώνου ΑΒΓ, να εξηγήσετε γιατί το τρίγωνο ΑΔΓ είναι ισοσκελές και να υπολογίσετε το μήκος της διχοτόμου ΑΔ.
4
Αν ΑΔ διχοτόμος τριγώνου ΑΒΓ, να αποδείξετε ότι:
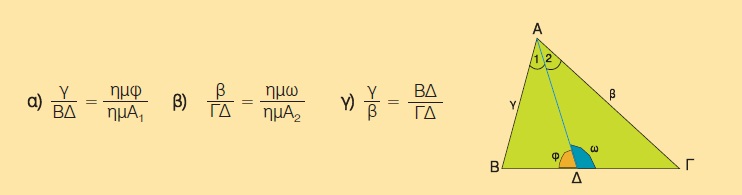
5
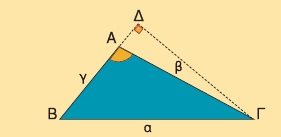
α) Να αποδείξετε ότι το εμβαδόν του τριγώνου ΑΒΓ του διπλανού σχήματος είναι 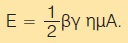
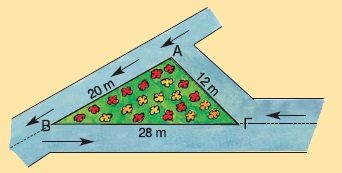
β) Να υπολογίσετε την γωνία 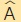 και το εμβαδόν του κήπου ΑΒΓ του διπλανού σχήματος. και το εμβαδόν του κήπου ΑΒΓ του διπλανού σχήματος.
6
α) Αν σ' ένα τρίγωνο ΑΒΓ ισχύει ημ2Α = ημ2Β + ημ2Γ, τότε να αποδείξετε ότι το τρίγωνο είναι ορθογώνιο.
β) Αν σ' ένα τρίγωνο ΑΒΓ ισχύει ημ(Β + Γ) + συν(Β - Γ) = 2, τότε να αποδείξετε ότι το τρίγωνο είναι ορθογώνιο και ισοσκελές.
7
Σε κάθε τρίγωνο ΑΒΓ να αποδείξετε ότι:
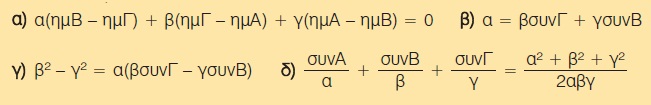
8
Να βρείτε τις πλευρές τριγώνου ΑΒΓ, αν τα μήκη τους είναι διαδοχικοί φυσικοί αριθμοί, η γ είναι η μικρότερη πλευρά και 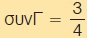
9
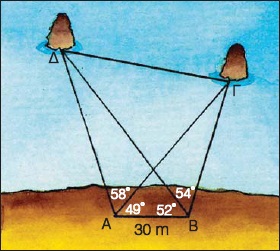
Δύο φίλοι τοποθέτησαν τα γωνιόμετρά τους στις θέσεις Α, Β μιας ακτής και παρατήρησαν δύο βράχους που προεξείχαν από την επιφάνεια της θάλασσας. Αν η απόσταση ΑΒ ήταν 30 m και τα αποτελέσματα των μετρήσεων τους φαίνονται στο παρακάτω σχήμα, τότε να υπολογίσετε την απόσταση των δύο βράχων. (Να χρησιμοποιήσετε τριγωνομετρικούς πίνακες).
|
|