1.3 Θεώρημα του Θαλή

Μαθαίνω το θεώρημα του Θαλή και πώς να το χρησιμοποιώ για τον υπολογισμό του μήκους ενός ευθυγράμμου τμήματος και του λόγου δύο τμημάτων.

ΔΡΑΣΤΗΡΙΟΤΗΤΑ

1. . Να χαράξετε μια ευθεία ε κάθετη στις γραμμές του τετραδίου σας και να επιλέξετε τρεις γραμμές του τετραδίου που να ορίζουν στην ε δύο ευθύγραμμα τμήματα, έτσι ώστε το ένα από αυτά να είναι διπλάσιο του άλλου.

2. Αν χαράξετε μια άλλη ευθεία ε΄ που δεν είναι κάθετη στις γραμμές του τετραδίου, τότε οι τρεις γραμμές που επιλέξατε προηγουμένως ορίζουν και στην ε΄ δύο ευθύγραμμα τμήματα, που το ένα είναι διπλάσιο του άλλου;

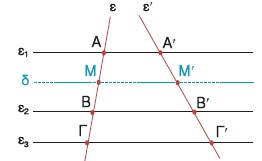
εικονα

Παίρνουμε τρεις παράλληλες ευθείες ε₁, ε₂, ε₃ που τέμνουν την ευθεία ε στα σημεία Α, Β, Γ αντιστοίχως, έτσι ώστε ΑΒ = 2 · ΒΓ.

Αν μια άλλη ευθεία ε΄ τέμνει τις ε₁, ε₂, ε₃ στα σημεία Α΄, Β΄, Γ΄ αντιστοίχως, τότε θα αποδείξουμε ότι και για τα ευθύγραμμα τμήματα Α΄Β΄, Β΄Γ΄ ισχύει μια ανάλογη σχέση. Δηλαδή Α΄Β΄ = 2 · Β΄Γ΄.

Πράγματι, αν από το μέσο Μ του ΑΒ φέρουμε την ευθεία δ παράλληλη προς τις ευθείες ε₁, ε₂, ε₃, τότε οι παράλληλες ευθείες ε₁, δ, ε₂, ε₃ ορίζουν στην ευθεία ε ίσα τμήματα, οπότε θα ορίζουν ίσα τμήματα και στην ευθεία ε΄. Δηλαδή ισχύει Α΄Μ΄ = Μ΄Β΄ = Β΄Γ΄ και επομένως Α΄Β΄ = 2 · Β΄Γ΄.

Παρατηρούμε λοιπόν ότι, αν ΑΒ = = 2 · ΒΓ θα ισχύει και Α΄Β΄ = 2 · Β΄Γ΄, οπότε

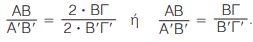
εικονα

Αυτό σημαίνει ότι τα ευθύγραμμα τμήματα ΑΒ, ΒΓ είναι ανάλογα προς τα ευθύγραμμα τμήματα Α΄Β΄, Β΄Γ΄.

Μικροπείραμα

Γενικά

Αν τρεις ή περισσότερες παράλληλες ευθείες τέμνουν δύο άλλες ευθείες, τότε τα τμήματα που ορίζονται στη μία είναι ανάλογα προς τα αντίστοιχα τμήματα που ορίζονται στην άλλη. Δηλαδή:

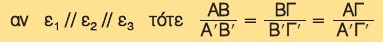
Η προηγούμενη πρόταση είναι γνωστή ως θεώρημα του Θαλή.

Από την ισότητα των τριών λόγων του Θεωρήματος του Θαλή έχουμε τις εξής αναλογίες

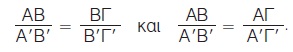
εικονα

Αν στις αναλογίες αυτές εναλλάξουμε τους μέσους όρους, τότε προκύπτουν και οι εξής αναλογίες

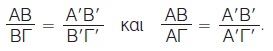
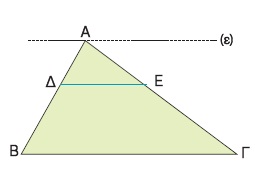
εικονα

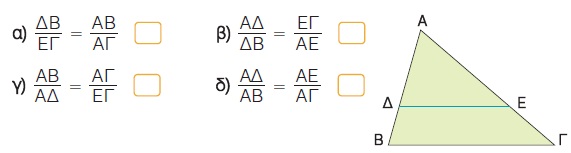
Για παράδειγμα, σ΄ ένα τρίγωνο ΑΒΓ, αν ΔΕ // ΒΓ και από την κορυφή Α φέρουμε ευθεία ε // ΒΓ, τότε οι παράλληλες ευθείες ε, ΔΕ, ΒΓ θα ορίζουν στις πλευρές ΑΒ, ΑΓ τμήματα ανάλογα.

Δηλαδή,

Αποδεικνύεται ακόμη ότι, αν ισχύει 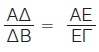εικόνα τότε ΔΕ // ΒΓ. Επομένως:

Για δύο σημεία Δ, Ε των πλευρών ΑΒ, ΑΓ αντιστοίχως ενός τριγώνου ΑΒΓ ισχύουν:

Μικροπείραμα Μικροπείραμα

ΠΑΡΑΔΕΙΓΜΑΤΑ − ΕΦΑΡΜΟΓΕΣ

Στο τρίγωνο ΑΒΓ είναι ΑΒ = 9, ΑΕ = 4 και ΕΓ = 6. Αν ΔΕ // ΒΓ να υπολογιστούν τα x, y.

Λύση

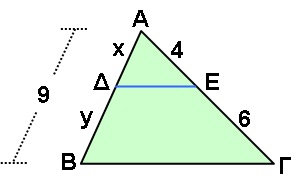
Στο τρίγωνο ΑΒΓ είναι ΔΕ // ΒΓ, οπότε από το θεώρημα του Θαλή έχουμε:

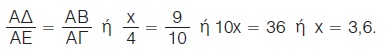
εικονα

Άρα y = 9 - 3,6 οπότε y = 5,4.

Μέσα από ένα οικόπεδο ΑΒΓΔ σχήματος τραπεζίου με ΑΔ = 50 m και ΒΓ = 60 m πέρασε ένας δρόμος παράλληλος προς τις πλευρές του ΑΒ, ΓΔ που είχε πλάτος 10 m και χώρισε το οικόπεδο στα δύο, όπως φαίνεται στο παρακάτω σχήμα. Αν είναι ΑΕ = 22 m και ΖΔ = 18 m, να υπολογιστούν τα μήκη των ευθυγράμμων τμημάτων ΒΗ, ΘΓ, ΗΘ.

Λύση

Επειδή ΑΒ // ΕΗ // ΔΓ από το Θεώρημα Θαλή έχουμε:

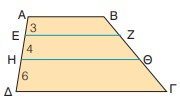
εικονα

ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ

Αν ΑΒ, ΕΖ, ΗΘ, ΔΓ είναι παράλληλες, να συμπληρώσετε τις ισότητες:

Αν ΔΕ // ΒΓ, να χαρακτηρίσετε τις προτάσεις της επόμενης σελίδας με (Σ), αν είναι σωστές ή με (Λ), αν είναι λανθασμένες:

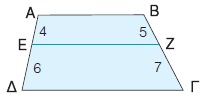
Ένας μαθητής ισχυρίστηκε ότι στο διπλανό τραπέζιο ΑΒΓΔ η ΕΖ είναι παράλληλη στις βάσεις του. Είχε δίκιο; Να αιτιολογήσετε την απάντησή σας.

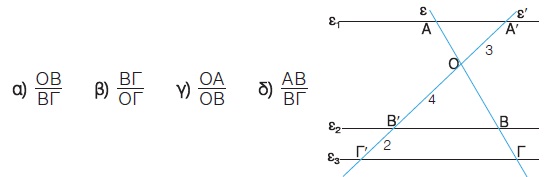
Στο διπλανό σχήμα είναι ε₁ // ε₂ // ε₃. Να υπολογίσετε τους λόγους:

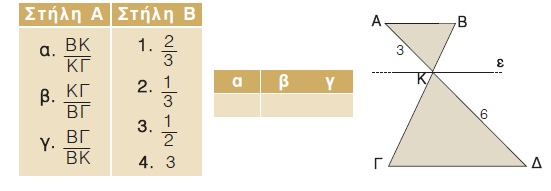
εικονα

Στο διπλανό σχήμα είναι ΑΒ // ε // ΓΔ. Να συμπληρώσετε τον παρακάτω πίνακα αντιστοιχίζοντας σε κάθε λόγο της στήλης Α τον ίσο του αριθμό από τη στήλη Β.

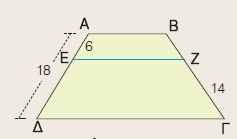
εικονα

ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ − ΠΡΟΒΛΗΜΑΤΑ

Στο τραπέζιο ΑΒΓΔ η ΕΖ είναι παράλληλη στις βάσεις του. Να υπολογίσετε το ευθύγραμμο τμήμα ΒΖ.

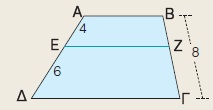
Στο τραπέζιο ΑΒΓΔ η ΕΖ είναι παράλληλη στις βάσεις του. Να υπολογίσετε τα ευθύγραμμα τμήματα ΒΖ και ΖΓ.

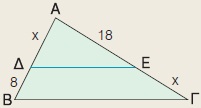
Στο τρίγωνο ΑΒΓ είναι ΔΕ // ΒΓ. Να υπολογίσετε το x.

Μικροπείραμα

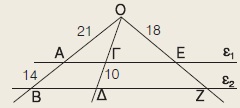
Στο διπλανό σχήμα είναι ε₁ // ε₂. Να υπολογίσετε τα ευθύγραμμα τμήματα ΟΓ και ΕΖ.

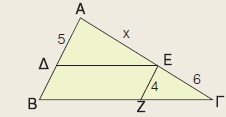
Στο τρίγωνο ΑΒΓ είναι ΔΕ // ΒΓ, ΕΖ // ΑΒ. Να υπολογίσετε το x.

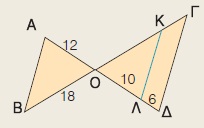
Στο διπλανό σχήμα είναι ΑΒ // ΚΛ // ΓΔ. Να υπολογίσετε τα ευθύγραμμα τμήματα ΟΚ και ΚΓ.

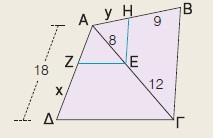
Στο διπλανό σχήμα είναι ΕΖ // ΔΓ και ΕΗ // ΒΓ. Να υπολογίσετε τα x, y.

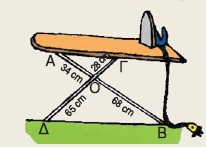
Κάποιος συναρμολόγησε μια πτυσσόμενη σιδερώστρα, όπως φαίνεται στο διπλανό σχήμα και διαπίστωσε ότι η σανίδα δεν ήταν οριζόντια. Πού έγινε το λάθος;