- Μαθαίνω πότε παράλληλες ευθείες ορίζουν ίσα τμήματα σε μια ευθεία που τις τέμνει.
- Μαθαίνω να διαιρώ ένα ευθύγραμμο τμήμα σε ν ίσα τμήματα.
- Μαθαίνω τι ονομάζεται λόγος δύο ευθυγράμμων τμημάτων και πώς υπολογίζεται.
- Μαθαίνω πότε δύο ευθύγραμμα τμήματα είναι ανάλογα προς δύο άλλα τμήματα.
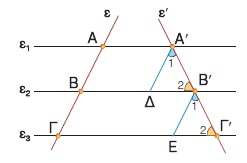
Παίρνουμε τρεις παράλληλες ευθείες ε1, ε2, ε3 που τέμνουν την ευθεία ε στα σημεία Α, Β, Γ αντιστοίχως, έτσι ώστε τα ευθύγραμμα τμήματα ΑΒ, ΒΓ να είναι ίσα μεταξύ τους.
Αν μια άλλη ευθεία ε΄ τέμνει τις ε1, ε2, ε3 στα σημεία Α΄, Β΄, Γ΄ αντιστοίχως, τότε θα αποδείξουμε ότι και τα ευθύγραμμα τμήματα Α΄Β΄, ´ô είναι ίσα μεταξύ τους.
Πράγματι, αν φέρουμε Α΄Δ // ε, Β΄Ε // ε και συγκρίνουμε τα τρίγωνα Α΄Β΄Δ και ´ôŠπαρατηρούμε ότι έχουν:
- Α΄Δ = Β΄Ε γιατί Α΄Δ = ΑΒ, Β΄Ε = ΒΓ ως απέναντι πλευρές των παραλληλογράμμων ΑΑ΄ΔΒ, ΒΒ΄ΕΓ αντιστοίχως και από την υπόθεση έχουμε ΑΒ = ΒΓ.
- Β2΄ = Γ2΄ γιατί είναι εντός εκτός και επί τα αυτά μέρη των παραλλήλων ε2, ε3 που τέμνονται από την ε΄.
- Α1΄ = Β1΄ γιατί είναι εντός εκτός και επί τα αυτά μέρη των παραλλήλων Α΄Δ, Β΄Ε που τέμνονται από την ε΄.
Τα τρίγωνα αυτά έχουν δύο γωνίες ίσες, οπότε θα έχουν και την τρίτη γωνία τους ίση, επομένως είναι ίσα, γιατί έχουν μια πλευρά ίση και τις προσκείμενες στην πλευρά αυτή γωνίες ίσες μία προς μία. Άρα, θα έχουν και τα υπόλοιπα αντίστοιχα στοιχεία τους ίσα, οπότε Α'Β' = Β'Γ'. Αποδείξαμε, λοιπόν, ότι:
Αν παράλληλες ευθείες ορίζουν ίσα τμήματα σε μια ευθεία, τότε θα ορίζουν ίσα τμήματα και σε οποιαδήποτε άλλη ευθεία που τις τέμνει.
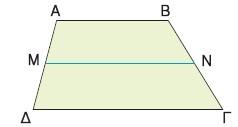
Για παράδειγμα, σ´ ένα τραπέζιο ΑΒΓΔ (ΑΒ // ΓΔ) αν από το μέσο Μ της ΑΔ φέρουμε ευθεία ΜΝ παράλληλη προς τις βάσεις του, τότε οι παράλληλες ΑΒ, ΜΝ, ΔΓ, αφού ορίζουν ίσα τμήματα στην ΑΔ, θα ορίζουν ίσα τμήματα και στην ΒΓ. Άρα ΒΝ = ΝΓ.
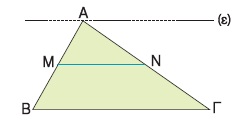
Ομοίως, σ´ ένα τρίγωνο ΑΒΓ, αν από την κορυφή Α φέρουμε ευθεία ε // ΒΓ και από το μέσο Μ της ΑΒ φέρουμε ΜΝ // ΒΓ, τότε οι παράλληλες ε, ΜΝ, ΒΓ αφού ορίζουν ίσα τμήματα στην ΑΒ, θα ορίζουν ίσα τμήματα και στην ΑΓ. Άρα ΑΝ = ΝΓ. Αποδείξαμε, λοιπόν, ότι:
Αν από το μέσο μιας πλευράς ενός τριγώνου φέρουμε ευθεία παράλληλη προς μία άλλη πλευρά του, τότε αυτή διέρχεται από το μέσο της τρίτης πλευράς του.
Αν πάρουμε ένα ευθύγραμμο τμήμα ΑΒ = 5 cm και θέλουμε να το διαιρέσουμε σε τρία ίσα τμήματα, τότε το μήκος κάθε τμήματος θα είναι 1,66... cm, οπότε καθένα από αυτά δεν προσδιορίζεται με ακρίβεια.
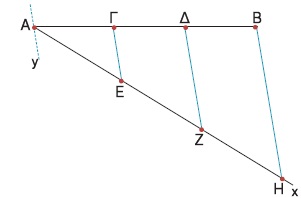
Μπορούμε όμως να διαιρέσουμε το ευθύγραμμο τμήμα ΑΒ σε τρία ίσα τμήματα με ακρίβεια, αν εργαστούμε με τη βοήθεια κανόνα και διαβήτη ως εξής:
Από το σημείο Α φέρουμε μια τυχαία ημιευθεία Αx και πάνω σ' αυτήν παίρνουμε με το διαβήτη τρία διαδοχικά ίσα ευθύγραμμα τμήματα ΑΕ, ΕΖ, ΖΗ. Ενώνουμε τα σημεία Β, Η και από τα σημεία Ζ, Ε, Α φέρνουμε ΖΔ, ΕΓ, Αy παράλληλες προς τη ΒΗ. Οι παράλληλες αυτές ορίζουν στην Αx ίσα τμήματα, οπότε θα ορίζουν ίσα τμήματα και στην ΑΒ. Άρα έχουμε ΑΓ = ΓΔ = ΔΒ. Με τον ίδιο τρόπο μπορούμε να διαιρέσουμε το ευθύγραμμο ΑΒ σε 4, 5, 6, ..., ν ίσα τμήματα.
Μικροπείραμα  Μικροπείραμα Μικροπείραμα 
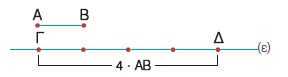
- Αν έχουμε ένα ευθύγραμμο τμήμα ΑΒ και σε μια ευθεία ε πάρουμε τέσσερα διαδοχικά ευθύγραμμα τμήματα που το καθένα είναι ίσο με ΑΒ, τότε κατασκευάζουμε το ευθύγραμμο τμήμα ΓΔ, για το οποίο λέμε ότι είναι ίσο με 4·ΑΒ και γράφουμε ΓΔ = 4·ΑΒ. Η ισότητα αυτή γράφεται και ως εξής:
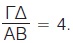
 Στην περίπτωση αυτή λέμε ότι ο λόγος του ευθύγραμμου τμήματος ΓΔ προς το ευθύγραμμο τμήμα ΑΒ είναι ο αριθμός 4. Στην περίπτωση αυτή λέμε ότι ο λόγος του ευθύγραμμου τμήματος ΓΔ προς το ευθύγραμμο τμήμα ΑΒ είναι ο αριθμός 4.
- Αν διαιρέσουμε ένα ευθύγραμμο τμήμα ΑΒ σε τρία ίσα ευθύγραμμα τμήματα ΑΓ, ΓΔ, ΔΒ, τότε λέμε ότι το τμήμα ΑΓ είναι ίσο με
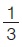 ·ΑΒ και γράφουμε: ·ΑΒ και γράφουμε:
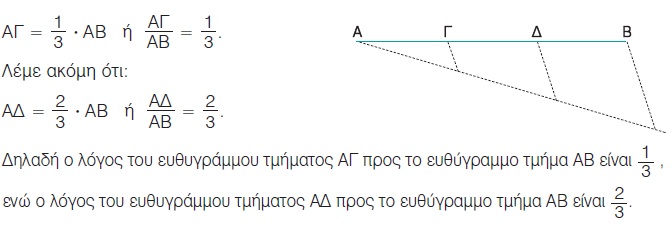
Συμπεραίνουμε, λοιπόν, ότι:
Ο λόγος ενός ευθύγραμμου τμήματος ΓΔ προς το ευθύγραμμο τμήμα ΑΒ συμβολίζεται 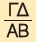 και είναι ο αριθμός λ, για τον οποίο ισχύει ΓΔ = λ · ΑΒ.
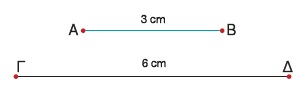 Αν πάρουμε τα ευθύγραμμα τμήματα ΑΒ = 3 cm και ΓΔ = 6 cm, τότε μπορούμε να διαπιστώσουμε ότι ο λόγος του ευθύγραμμου τμήματος ΑΒ προς το ευθύγραμμο τμήμα ΓΔ είναι Αν πάρουμε τα ευθύγραμμα τμήματα ΑΒ = 3 cm και ΓΔ = 6 cm, τότε μπορούμε να διαπιστώσουμε ότι ο λόγος του ευθύγραμμου τμήματος ΑΒ προς το ευθύγραμμο τμήμα ΓΔ είναι 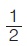 , δηλαδή είναι ίσος με το λόγο των μηκών τους , δηλαδή είναι ίσος με το λόγο των μηκών τους 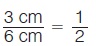 . .
Μικροπείραμα 
Γενικά
Ο λόγος δύο ευθυγράμμων τμημάτων είναι ίσος με το λόγο των μηκών τους, εφόσον έχουν μετρηθεί με την ίδια μονάδα μέτρησης.
Για παράδειγμα, αν έχουμε ΔΕ = 120 cm και ZH = 1,5 m, τότε
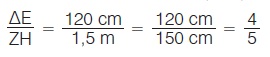
Παρατηρούμε, λοιπόν, ότι ο λόγος δύο ευθυγράμμων τμημάτων είναι ένας αριθμός που εκφράζει τη σχέση που συνδέει τα μήκη τους. Αν γνωρίζουμε λοιπόν το λόγο δύο ευθυγράμμων τμημάτων π.χ. 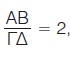 , αυτό σημαίνει ότι το μήκος του ΑΒ είναι διπλάσιο από το μήκος του ΓΔ, αλλά δε γνωρίζουμε το μήκος κάθε τμήματος, αφού είναι δυνατό να είναι ΑΒ = 80 cm και ΓΔ = 40 cm ή ΑΒ = 18 cm και ΓΔ = 9 cm κ.τ.λ. , αυτό σημαίνει ότι το μήκος του ΑΒ είναι διπλάσιο από το μήκος του ΓΔ, αλλά δε γνωρίζουμε το μήκος κάθε τμήματος, αφού είναι δυνατό να είναι ΑΒ = 80 cm και ΓΔ = 40 cm ή ΑΒ = 18 cm και ΓΔ = 9 cm κ.τ.λ.
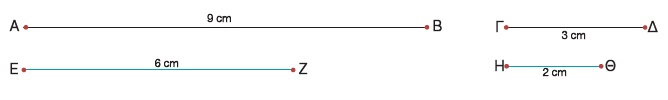
Αν πάρουμε τα ευθύγραμμα τμήματα ΑΒ = 9 cm και ΓΔ = = 3 cm, τότε ο λόγος του ΑΒ προς το ΓΔ είναι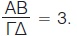 . Ομοίως, αν πάρουμε τα ευθύγραμμα τμήματα ΕΖ = 6 cm και . Ομοίως, αν πάρουμε τα ευθύγραμμα τμήματα ΕΖ = 6 cm και
ΗΘ = 2 cm, τότε ο λόγος του ΕΖ προς το ΗΘ είναι 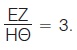 . .
Παρατηρούμε, λοιπόν, ότι 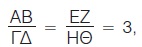 , δηλαδή ο λόγος του ΑΒ προς το ΓΔ είναι ίσος με το λόγο του ΕΖ προς το ΗΘ. Στην περίπτωση αυτή λέμε ότι τα ευθύγραμμα τμήματα ΑΒ, ΕΖ είναι ανάλογα προς τα ευθύγραμμα τμήματα ΓΔ, ΗΘ. , δηλαδή ο λόγος του ΑΒ προς το ΓΔ είναι ίσος με το λόγο του ΕΖ προς το ΗΘ. Στην περίπτωση αυτή λέμε ότι τα ευθύγραμμα τμήματα ΑΒ, ΕΖ είναι ανάλογα προς τα ευθύγραμμα τμήματα ΓΔ, ΗΘ.
Γενικά
Τα ευθύγραμμα τμήματα α, γ είναι ανάλογα προς τα ευθύγραμμα τμήματα β, δ, όταν ισχύει 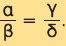
Η ισότητα 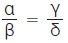 ονομάζεται αναλογία με όρους τα ευθύγραμμα τμήματα α, β, γ, δ. Τα ευθύγραμμα τμήματα α, δ ονομάζονται άκροι όροι, ενώ τα ευθύγραμμα τμήματα β, γ ονομάζονται μέσοι όροι της αναλογίας. ονομάζεται αναλογία με όρους τα ευθύγραμμα τμήματα α, β, γ, δ. Τα ευθύγραμμα τμήματα α, δ ονομάζονται άκροι όροι, ενώ τα ευθύγραμμα τμήματα β, γ ονομάζονται μέσοι όροι της αναλογίας.
Σε μια αναλογία με όρους τα ευθύγραμμα τμήματα α, β, γ, δ χρησιμοποιούμε τις γνωστές ιδιότητες των αναλογιών που ισχύουν και στους αριθμούς. Στην περίπτωση αυτή ως α, β, γ, δ θεωρούμε τα μήκη των ευθυγράμμων τμημάτων.
Οι σημαντικότερες ιδιότητες των αναλογιών είναι:
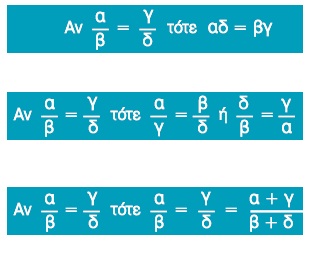
- Σε κάθε αναλογία το γινόμενο των άκρων όρων είναι ίσο με το γινόμενο των μέσων όρων.
- Σε κάθε αναλογία μπορούμε να εναλλάξουμε τους μέσους ή τους άκρους όρους και να προκύψει πάλι αναλογία.
- Λόγοι ίσοι μεταξύ τους είναι και ίσοι με το λόγο που έχει αριθμητή το άθροισμα των αριθμητών και παρονομαστή το άθροισμα των παρονομαστών.
|
 |
|