- Θυμάμαι ποια είναι τα στοιχεία ενός τριγώνου (κύρια - δευτερεύοντα) και τα είδη των τριγώνων.
- Μαθαίνω πότε δύο τρίγωνα είναι ίσα και ποια είναι τα κριτήρια ισότητας τρίγωνων.
- Μαθαίνω ποια είναι τα κριτήρια ισότητας ορθογωνίων τριγώνων.
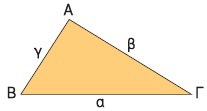
Σε κάθε τρίγωνο οι πλευρές και οι γωνίες του ονομάζονται κύρια στοιχεία του τριγώνου. Οι πλευρές ενός τριγώνου ΑΒΓ που βρίσκονται απέναντι από τις γωνίες του 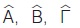 συμβολίζονται αντιστοίχως α, β, γ. συμβολίζονται αντιστοίχως α, β, γ.
Για τις γωνίες κάθε τριγώνου ισχύει

Η γωνία του τριγώνου που περιέχεται μεταξύ δύο πλευρών λέγεται περιεχόμενη γωνία των πλευρών αυτών, π.χ. περιεχόμενη γωνία των πλευρών ΑΒ, ΑΓ είναι η γωνία 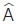 . Οι γωνίες του τριγώνου που έχουν κορυφές τα άκρα μιας πλευράς λέγονται προσκείμενες γωνίες της πλευράς αυτής π.χ. προσκείμενες γωνίες της πλευράς ΒΓ είναι οι . Οι γωνίες του τριγώνου που έχουν κορυφές τα άκρα μιας πλευράς λέγονται προσκείμενες γωνίες της πλευράς αυτής π.χ. προσκείμενες γωνίες της πλευράς ΒΓ είναι οι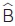 και και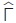 . Ένα τρίγωνο ανάλογα με το είδος των γωνιών του ονομάζεται: . Ένα τρίγωνο ανάλογα με το είδος των γωνιών του ονομάζεται:
Σε κάθε ορθογώνιο τρίγωνο η πλευρά που βρίσκεται απέναντι από την ορθή γωνία ονομάζεται υποτείνουσα, ενώ οι άλλες δύο ονομάζονται κάθετες πλευρές.
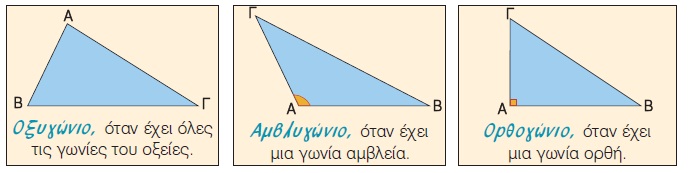
Ένα τρίγωνο ανάλογα με τις σχέσεις που συνδέονται οι πλευρές του ονομάζεται:
Σε ισοσκελές τρίγωνο ΑΒΓ με ΑΒ = ΑΓ η πλευρά ΒΓ ονομάζεται βάση του και το σημείο Α κορυφή του.
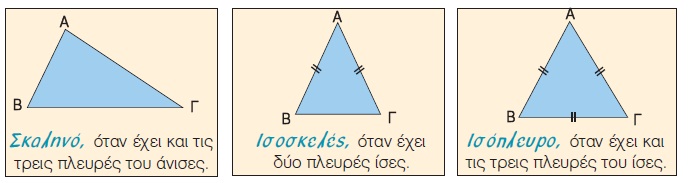
Σ΄ ένα τρίγωνο, εκτός από τα κύρια στοιχεία, υπάρχουν και τα δευτερεύοντα στοιχεία, που είναι οι διάμεσοι, οι διχοτόμοι και τα ύψη.
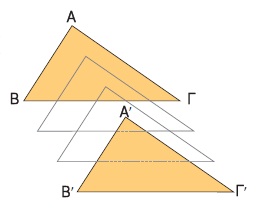
Αν μετατοπίσουμε ένα τρίγωνο ΑΒΓ σε μια άλλη θέση και θεωρήσουμε ότι κατά τη μετατόπισή του αυτό δε μεταβάλλεται, τότε οι κορυφές του Α, Β, Γ θα πάρουν τις θέσεις των σημείων Α΄, Β΄, Γ΄ αντιστοίχως και το τρίγωνο ΑΒΓ θα πάρει τη θέση του τριγώνου Α΄Β΄Γ΄. Αφού τα τρίγωνα ΑΒΓ και Α΄Β΄Γ΄ ταυτίζονται, τότε οι αντίστοιχες πλευρές και γωνίες τους θα είναι ίσες, αφού και αυτές ταυτίζονται. Έτσι έχουμε:
ΑΒ = Α΄Β΄, ΒΓ = ´ô, ΑΓ = Α΄Γ΄ και
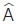 = =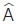 ΄ , ΄ , 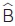 = =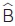 ΄ , ΄ , 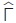 = = 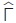 ΄ . ΄ .
Δύο τρίγωνα ΑΒΓ και Α΄Β΄Γ΄, για τα οποία ισχύουν οι προηγούμενες ισότητες, λέμε ότι είναι ίσα. Δηλαδή
- Αν δύο τρίγωνα έχουν τις πλευρές τους ίσες μία προς μία και τις αντίστοιχες γωνίες τους ίσες, τότε είναι ίσα.
Ισχύει ακόμη και το αντίστροφο. Δηλαδή
- Αν δύο τρίγωνα είναι ίσα, τότε θα έχουν τις πλευρές τους και τις αντίστοιχες γωνίες τους ίσες μία προς μία.
Στο εξής σε κάθε μετατόπιση τριγώνου θα θεωρούμε ότι αυτό δε μεταβάλλεται. Αυτό σημαίνει ότι, αν έχουμε δύο ίσα τρίγωνα και μετατοπίσουμε κατάλληλα το ένα από αυτά, τότε τα τρίγωνα ταυτίζονται.
Για να αποδείξουμε ότι δύο τρίγωνα είναι ίσα δεν είναι απαραίτητο να αποδείξουμε ότι έχουν όλες τις πλευρές τους και τις αντίστοιχες γωνίες ίσες μία προς μία.
Στη συνέχεια, θα μάθουμε προτάσεις με τις οποίες διαπιστώνουμε ότι και με λιγότερα στοιχεία είναι δυνατόν να διακρίνουμε αν δύο τρίγωνα είναι ίσα. Οι προτάσεις αυτές είναι γνωστές ως κριτήρια ισότητας τριγώνων.
1ο κριτήριο ισότητας (Π - Γ - Π)
Για δύο τρίγωνα ισχύει η παρακάτω βασική ιδιότητα ισότητας
Αν δύο τρίγωνα έχουν δύο πλευρές ίσες μία προς μία και την περιεχόμενη γωνία τους ίση, τότε είναι ίσα.
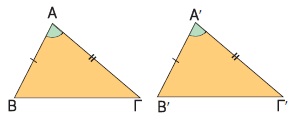 Πράγματι, σχεδιάζουμε δύο τρίγωνα ΑΒΓ και Α΄Β΄Γ΄ που να έχουν δύο πλευρές ίσες ΑΒ = Α΄Β΄, ΑΓ = Α΄Γ΄ και την περιεχόμενη γωνία τους ίση Πράγματι, σχεδιάζουμε δύο τρίγωνα ΑΒΓ και Α΄Β΄Γ΄ που να έχουν δύο πλευρές ίσες ΑΒ = Α΄Β΄, ΑΓ = Α΄Γ΄ και την περιεχόμενη γωνία τους ίση 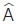 = =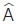 ΄. ΄.
Αν μετατοπίσουμε το τρίγωνο ΑΒΓ, έτσι ώστε η γωνία 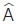 να συμπέσει με την ίση της γωνία να συμπέσει με την ίση της γωνία 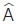 ΄ και η πλευρά ΑΒ να συμπέσει με την ίση της πλευρά Α΄Β΄, τότε η πλευρά ΑΓ θα συμπέσει με την ίση της πλευρά Α΄Γ΄ και οι κορυφές Β, Γ θα συμπέσουν με τις κορυφές Β΄, Γ΄ αντιστοίχως. Άρα τα τρίγωνα ΑΒΓ και Α΄Β΄Γ΄ ταυτίζονται, οπότε είναι ίσα. ΄ και η πλευρά ΑΒ να συμπέσει με την ίση της πλευρά Α΄Β΄, τότε η πλευρά ΑΓ θα συμπέσει με την ίση της πλευρά Α΄Γ΄ και οι κορυφές Β, Γ θα συμπέσουν με τις κορυφές Β΄, Γ΄ αντιστοίχως. Άρα τα τρίγωνα ΑΒΓ και Α΄Β΄Γ΄ ταυτίζονται, οπότε είναι ίσα.
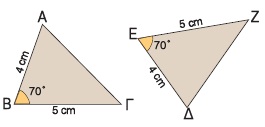 Για παράδειγμα, τα τρίγωνα ΑΒΓ και ΔΕΖ του διπλανού σχήματος είναι ίσα, αφού έχουν δύο πλευρές ίσες (ΑΒ = ΔΕ = 4 cm, ΒΓ = ΕΖ = 5 cm) και την περιεχόμενη γωνία τους ίση ( Για παράδειγμα, τα τρίγωνα ΑΒΓ και ΔΕΖ του διπλανού σχήματος είναι ίσα, αφού έχουν δύο πλευρές ίσες (ΑΒ = ΔΕ = 4 cm, ΒΓ = ΕΖ = 5 cm) και την περιεχόμενη γωνία τους ίση (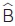 = = 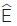 = 70º). Επομένως, τα τρίγωνα θα έχουν και τα υπόλοιπα αντίστοιχα στοιχεία τους ίσα, δηλαδή = 70º). Επομένως, τα τρίγωνα θα έχουν και τα υπόλοιπα αντίστοιχα στοιχεία τους ίσα, δηλαδή
ΑΓ = ΔΖ, 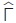 = = 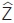 και και 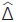 = = 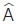 . .
Παρατηρούμε ότι οι ίσες γωνίες 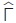 , , 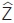 βρίσκονται απέναντι από τις ίσες πλευρές ΑΒ, ΕΔ. βρίσκονται απέναντι από τις ίσες πλευρές ΑΒ, ΕΔ.
Μικροπείραμα  Μικροπείραμα Μικροπείραμα  Μικροπείραμα Μικροπείραμα 
Γενικά:
Σε ίσα τρίγωνα απέναντι από ίσες πλευρές βρίσκονται ίσες γωνίες.
2ο κριτήριο ισότητας (Γ - Π - Γ).
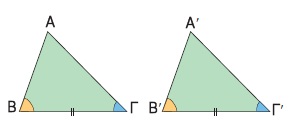
Σχεδιάζουμε δύο τρίγωνα ΑΒΓ και Α΄Β΄Γ΄ που να έχουν μία πλευρά ίση ΒΓ = ´ô και τις προσκείμενες στην πλευρά αυτή γωνίες ίσες 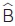 = =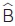 ΄ και ΄ και 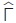 = =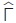 ΄. Αν μετατοπίσουμε το τρίγωνο ΑΒΓ, έτσι ώστε η πλευρά του ΒΓ να συμπέσει με την ίση της πλευρά Β΄Γ΄ και η γωνία ΄. Αν μετατοπίσουμε το τρίγωνο ΑΒΓ, έτσι ώστε η πλευρά του ΒΓ να συμπέσει με την ίση της πλευρά Β΄Γ΄ και η γωνία 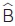 να συμπέσει με τη ίση της γωνία να συμπέσει με τη ίση της γωνία 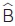 ΄, τότε η γωνία ΄, τότε η γωνία 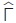 θα συμπέσει με την ίση της γωνία θα συμπέσει με την ίση της γωνία 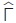 ΄ και η κορυφή Α θα συμπέσει με την κορυφή Α΄. ΄ και η κορυφή Α θα συμπέσει με την κορυφή Α΄.
Άρα τα τρίγωνα ΑΒΓ και Α΄Β΄Γ΄ ταυτίζονται, οπότε είναι ίσα. Επομένως
Αν δύο τρίγωνα έχουν μία πλευρά ίση και τις προσκείμενες στην πλευρά αυτή γωνίες ίσες μία προς μία, τότε είναι ίσα.
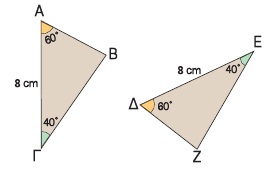
Για παράδειγμα, τα τρίγωνα ΑΒΓ και ΔΕΖ του διπλανού σχήματος είναι ίσα, αφού έχουν μία πλευρά ίση (ΑΓ = ΔΕ = 8 cm) και τις προσκείμενες στην πλευρά αυτή γωνίες ίσες ( 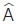 = = 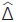 = 60º, = 60º, 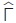 = =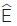 = 40º). Επομένως τα τρίγωνα θα έχουν και τα υπόλοιπα αντίστοιχα στοιχεία τους ίσα, δηλαδή = 40º). Επομένως τα τρίγωνα θα έχουν και τα υπόλοιπα αντίστοιχα στοιχεία τους ίσα, δηλαδή
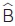 = = 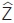 , ΑΒ = ΔΖ, ΒΓ = ΕΖ. , ΑΒ = ΔΖ, ΒΓ = ΕΖ.
Παρατηρούμε ότι οι ίσες πλευρές ΑΒ, ΔΖ βρίσκονται απέναντι από τις ίσες γωνίες 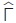 , , 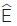 . Γενικά: . Γενικά:
Μικροπείραμα  Μικροπείραμα Μικροπείραμα  Μικροπείραμα Μικροπείραμα 
Σε ίσα τρίγωνα απέναντι από ίσες γωνίες βρίσκονται ίσες πλευρές.
3ο κριτήριο ισότητας (Π - Π - Π)
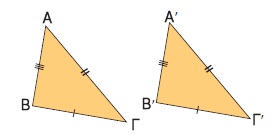
Σχεδιάζουμε δύο τρίγωνα ΑΒΓ και Α΄Β΄Γ΄ που να έχουν και τις τρεις πλευρές τους ίσες
(ΑΒ = Α΄Β΄, ΒΓ = ´ô, ΑΓ = Α΄Γ΄).
Αν μετατοπίσουμε κατάλληλα το τρίγωνο ΑΒΓ, τότε αυτό ταυτίζεται με το τρίγωνο Α΄Β΄Γ΄, οπότε τα τρίγωνα είναι ίσα. Επομένως
Αν δύο τρίγωνα έχουν τις πλευρές τους ίσες μία προς μία, τότε είναι ίσα.
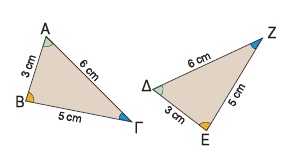
Για παράδειγμα, τα τρίγωνα ΑΒΓ και ΔΕΖ του διπλανού σχήματος είναι ίσα, αφού έχουν και τις τρεις πλευρές τους ίσες, ΑΒ = ΔΕ = 3 cm, ΑΓ = ΔΖ = 6 cm και ΒΓ = ΕΖ = 5 cm. Άρα θα έχουν και τα υπόλοιπα αντίστοιχα στοιχεία τους ίσα, δηλαδή
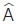 = = 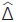 , , 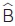 = =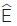 και και 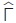 = = 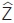 . .
Μικροπείραμα  Μικροπείραμα Μικροπείραμα 
Τα προηγούμενα κριτήρια ισότητας τριγώνων μπορούμε να τα εφαρμόσουμε και στα ορθογώνια τρίγωνα.
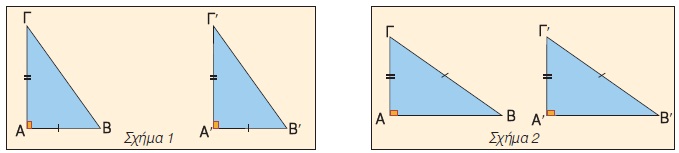
Στο σχήμα 1 τα ορθογώνια τρίγωνα ΑΒΓ και Α΄Β΄Γ΄ είναι ίσα, γιατί έχουν τις κάθετες πλευρές τους ίσες μία προς μία και την περιεχόμενη γωνία τους ίση, αφού αυτή είναι ορθή.
Στο σχήμα 2 τα ορθογώνια τρίγωνα ΑΒΓ και Α΄Β΄Γ΄ έχουν την υποτείνουσα και μια κάθετη πλευρά ίση και όπως προκύπτει από το Πυθαγόρειο θεώρημα θα έχουν και την τρίτη πλευρά τους ίση. Άρα τα τρίγωνα θα είναι ίσα, αφού έχουν και τις τρεις πλευρές τους ίσες μία προς μία.
Οι δύο αυτές περιπτώσεις συνοψίζονται στο εξής κριτήριο ισότητας ορθογωνίων τριγώνων.
Αν δύο ορθογώνια τρίγωνα έχουν δύο αντίστοιχες πλευρές τους ίσες μία προς μία, τότε είναι ίσα.
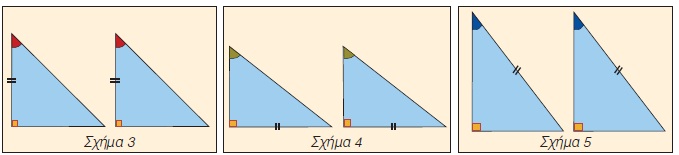
Στο σχήμα 3 τα ορθογώνια τρίγωνα είναι ίσα, γιατί έχουν μία πλευρά ίση και τις προσκείμενες στην πλευρά αυτή γωνίες ίσες μία προς μία.
Στα σχήματα 4 και 5 τα ορθογώνια τρίγωνα έχουν δύο γωνίες ίσες μία προς μία, οπότε θα έχουν και την τρίτη γωνία τους ίση, αφού το άθροισμα των γωνιών ενός τριγώνου είναι 180ο. Άρα είναι ίσα γιατί έχουν μία πλευρά ίση και τις προσκείμενες στην πλευρά αυτή γωνίες ίσες μία προς μία.
Ο τρεις αυτές περιπτώσεις συνοψίζονται στο εξής κριτήριο ισότητας των ορθογωνίων τριγώνων. Αν δύο ορθογώνια τρίγωνα έχουν μία αντίστοιχη πλευρά ίση και μία αντίστοιχη οξεία γωνία ίση, τότε είναι ίσα.
Από τα προηγούμενα κριτήρια ισότητας ορθογωνίων τριγώνων διαπιστώνουμε ότι:
Δύο ορθογώνια τρίγωνα είναι ίσα, όταν έχουν
- δύο αντίστοιχες πλευρές ίσες μία προς μία ή
- μία αντίστοιχη πλευρά ίση και μία αντίστοιχη οξεία γωνία ίση.
|