- Μαθαίνω τι ονομάζεται πείραμα τύχης, ποιός είναι ο δειγματικός χώρος του και πώς αυτός προσδιορίζεται.
- Μαθαίνω τι ονομάζεται ενδεχόμενο ενός πειράματος τύχης, πότε πραγματοποιείται και πότε είναι βέβαιο ή αδύνατο.
- Γνωρίζω πως γίνονται οι πράξεις μεταξύ ενδεχομένων και ποια ενδεχόμενα ονομάζονται ασυμβίβαστα.
Σε πολλές περιπτώσεις, όταν κάνουμε ένα πείραμα, μπορούμε με βεβαιότητα να προβλέψουμε το αποτέλεσμά του. Για παράδειγμα:
− Αν μετρήσουμε τη θερμοκρασία μιας ποσότητας καθαρού νερού που βράζει, είμαστε βέβαιοι ότι η ένδειξη του θερμομέτρου θα είναι 100º Κελσίου.
− Αν επιλέξουμε ένα τυχαίο άρτιο αριθμό και τον διαιρέσουμε με το 2, είμαστε επίσης βέβαιοι ότι το υπόλοιπο της διαίρεσης θα είναι μηδέν.
Υπάρχουν όμως και πειράματα, τα οποία όσες φορές και αν τα επαναλάβουμε, δεν μπορούμε να προβλέψουμε το αποτέλεσμά τους με απόλυτη βεβαιότητα. Ένα τέτοιο πείραμα λέγεται πείραμα τύχης. Για παράδειγμα,
− Αν ρίξουμε ένα ζάρι δεν είμαστε σε θέση κάθε φορά να προβλέψουμε την ένδειξή του, αν και γνωρίζουμε ότι το σύνολο των δυνατών αποτελεσμάτων του είναι το {1, 2, 3, 4, 5, 6}
Το σύνολο αυτό συμβολίζεται με Ω και ονομάζεται δειγματικός χώρος του πειράματος.
Γενικά
Δειγματικός χώρος ενός πειράματος τύχης ονομάζεται το σύνολο των δυνατών αποτελεσμάτων του και συμβολίζεται με Ω.
Για παράδειγμα, κατά τη ρίψη ενός νομίσματος τα δυνατά αποτελέσματα είναι κεφαλή (Κ) και γράμματα (Γ), οπότε ο δειγματικός χώρος του πειράματος είναι Ω = {Κ, Γ}. Το πλήθος των στοιχείων ενός δειγματικού χώρου Ω συμβολίζεται με N(Ω). Π.χ. στη ρίψη ενός ζαριού είναι Ν(Ω) = 6, ενώ στη ρίψη ενός νομίσματος είναι Ν(Ω) = 2.
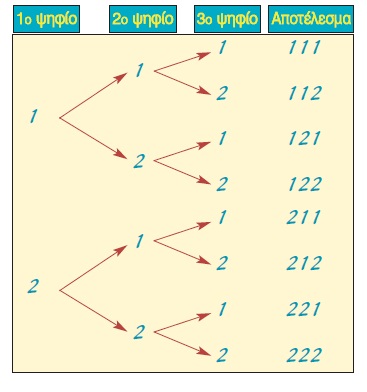
Σε πολλά πειράματα τύχης, όπως στη ρίψη ενός ζαριού ή ενός νομίσματος, μπορούμε να προσδιορίσουμε το δειγματικό χώρο εύκολα και άμεσα. Υπάρχουν όμως και πειράματα τύχης στα οποία προσδιορίζουμε ευκολότερα το δειγματικό τους χώρο, αν εφαρμόσουμε ειδικές τεχνικές ή μεθόδους. Για παράδειγμα, αν επιλέξουμε στην τύχη ένα τριψήφιο αριθμό που τα ψηφία του είναι 1 ή 2, για να προσδιορίσουμε το δειγματικό χώρο εργαζόμαστε ως εξής: Γράφουμε ποιο μπορεί να είναι το πρώτο ψηφίο και σε κάθε περίπτωση γράφουμε ποιο μπορεί να είναι το δεύτερο ψηφίο κ.ο.κ.
Με το παρακάτω διάγραμμα, που ονομάζεται δεντροδιάγραμμα, βρίσκουμε ευκολότερα όλα τα στοιχεία του δειγματικού χώρου. Ο δειγματικός χώρος Ω αποτελείται από όλους τους τριψήφιους αριθμούς με ψηφία 1 ή 2, δηλαδή είναι:
Ω = {111, 112, 121, 122, 211, 212, 221, 222}, και περιέχει 8 στοιχεία (Ν(Ω) = 8). |
 |
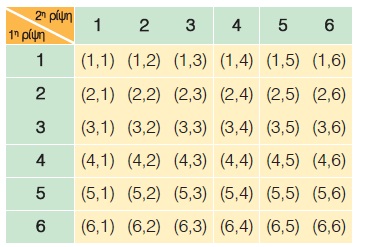
| Αν ρίξουμε ένα ζάρι δύο φορές και σημειώσουμε κάθε φορά την ένδειξή του, τότε για να προσδιορίσουμε ευκολότερα το δειγματικό χώρο, χρησιμοποιούμε τον παρακάτω πίνακα. Ο δειγματικός χώρος Ω αποτελείται από όλα τα διατεταγμένα ζεύγη του πίνακα, δηλαδή είναι: Ω = {(1, 1), (1, 2), (1, 3), …, (6, 5), (6,6)}, και περιέχει 36 στοιχεία (Ν(Ω) = 36). |
 |
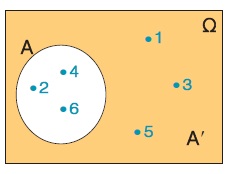
Αν ρίξουμε ένα ζάρι, γνωρίζουμε ότι ο δειγματικός χώρος είναι Ω = {1, 2, 3, 4, 5, 6}. Το σύνολο Α = {2, 4, 6}, που είναι υποσύνολο του Ω, ονομάζεται ενδεχόμενο του πειράματος και συγκεκριμένα είναι το ενδεχόμενο να φέρουμε άρτιο αριθμό. Ομοίως, το Β = {1, 2, 3} είναι το ενδεχόμενο να φέρουμε αριθμό μικρότερο του 4.
Γενικά
Ενδεχόμενο ενός πειράματος τύχης ονομάζεται κάθε υποσύνολο του δειγματικού χώρου Ω.
Αν ρίξουμε ένα ζάρι και φέρουμε τον αριθμό 6, που ανήκει στο σύνολο Α = {2, 4, 6}, τότε λέμε ότι το ενδεχόμενο Α πραγματοποιείται. Το ενδεχόμενο όμως Α πραγματοποιείται ακόμη και αν κατά τη συγκεκριμένη εκτέλεση του πειράματος εκτός από 6 φέρουμε 2 ή 4. Γι´ αυτό τα στοιχεία 2, 4, 6 του ενδεχομένου Α ονομάζονται ευνοϊκές περιπτώσεις για την πραγματοποίησή του.
Για ένα ενδεχόμενο Α, το πλήθος των ευνοϊκών του περιπτώσεων, δηλαδή το πλήθος των στοιχείων του, συμβολίζεται με Ν(Α). Για το ενδεχόμενο Α = {2, 4, 6} είναι Ν(Α) = 3.
Βέβαιο - Αδύνατο ενδεχόμενο
Αν ρίξουμε ένα ζάρι, τότε το ενδεχόμενο να φέρουμε ένδειξη μικρότερη του 7 είναι το Ω = {1, 2, 3, 4, 5, 6}. Το ενδεχόμενο αυτό πραγματοποιείται σε οποιαδήποτε εκτέλεση του πειράματος και γι´ αυτό ονομάζεται βέβαιο ενδεχόμενο.
Το ενδεχόμενο όμως να φέρουμε ένδειξη μεγαλύτερη του 6 είναι Ø. Το ενδεχόμενο αυτό δεν πραγματοποιείται σε καμία εκτέλεση του πειράματος και γι´ αυτό ονομάζεται αδύνατο ενδεχόμενο.
Πράξεις με ενδεχόμενα
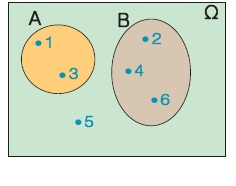
Όπως είδαμε, το ενδεχόμενο είναι σύνολο, οπότε παριστάνεται και με διάγραμμα Venn. Οι πράξεις μεταξύ ενδεχομένων γίνονται όπως και οι πράξεις μεταξύ συνόλων. Έτσι έχουμε:
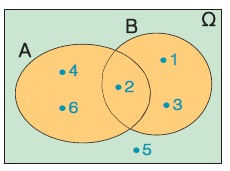
- Ένωση δύο ενδεχομένων Α, Β ονομάζεται το ενδεχόμενο Α U Β που πραγματοποιείται, όταν πραγματοποιείται ένα τουλάχιστον από τα Α, Β.
Π.χ. αν Α = {2, 4, 6} και Β = {1, 2, 3}, τότε
Α U Β = {1, 2, 3, 4, 5, 6}.
|
 |
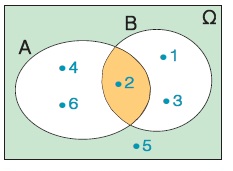
- Τομή δύο ενδεχομένων Α, Β ονομάζεται το ενδεχόμενο Α ∩ Β που πραγματοποιείται, όταν πραγματοποιούνται ταυτόχρονα το Α και το Β.
Π.χ. αν Α = {2, 4, 6} και Β = {1, 2, 3}, τότε
Α ∩ Β = {2}. |
 |
- Συμπλήρωμα ενός ενδεχομένου Α ονομάζεται το ενδεχόμενο Α΄ που πραγματοποιείται, όταν δεν πραγματοποιείται το Α.
Π.χ. στο πείραμα τύχης «ρίψη ενός ζαριού» αν
Α = {2, 4, 6}, τότε Α΄ = {1, 3, 5}.
|
 |
Ασυμβίβαστα ενδεχόμενα
Σ´ ένα πείραμα τύχης δύο ενδεχόμενα Α, Β είναι δυνατόν να μην έχουν κανένα κοινό στοιχείο, δηλαδή να ισχύει
Α ∩ Β = Ø.
Π.χ. στη ρίψη ενός ζαριού, τα ενδεχόμενα Α = {1, 3} και Β = {2, 4, 6} δεν έχουν κανένα κοινό στοιχείο, οπότε σε οποιαδήποτε εκτέλεση του πειράματος δεν είναι δυνατόν να πραγματοποιηθούν ταυτόχρονα. Στην περίπτωση αυτή λέμε ότι τα ενδεχόμενα Α και Β είναι ασυμβίβαστα.
Γενικά
Δύο ενδεχόμενα Α και Β ονομάζονται ασυμβίβαστα, όταν Α ∩ Β = Ø
|
1
Σ´ ένα τουρνουά σκακιού ένας παίκτης αποκλείεται από τη συνέχεια των αγώνων, αν ηττηθεί μία φορά ή φέρει δύο ισοπαλίες. Αν ένας παίκτης έδωσε το πολύ τρεις αγώνες, ποια είναι τα αποτελέσματα που θα μπορούσε να έχει φέρει μέχρι εκείνη τη στιγμή;
Λύση
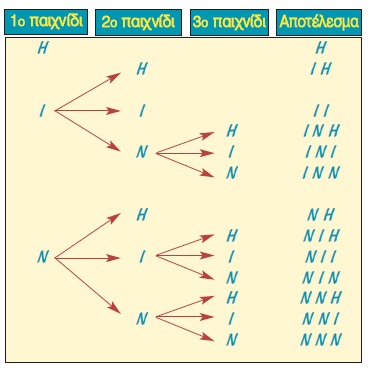
Το πιθανό αποτέλεσμα ενός σκακιστή για κάθε παιχνίδι είναι ήττα (Η), ισοπαλία (I) ή νίκη (Ν). Τα δυνατά αποτελέσματα που έφερε ένας παίκτης που έδωσε το πολύ τρεις αγώνες, προκύπτουν ευκολότερα από το παραπάνω διάγραμμα. Το σύνολο όλων των αποτελεσμάτων είναι:
Ω = {Η, ΙΗ, II, ΙΝΗ, INI, ΙΝΝ, ΝΗ, ΝΙΗ, ΝΙΙ, ΝΙΝ, ΝΝΗ, ΝΜ, ΝΝΝ}
2
Σ´ ένα κουτί υπάρχουν 4 μπάλες αριθμημένες από το 1 έως το 4. Επιλέγουμε στην τύχη μια μπάλα, καταγράφουμε τον αριθμό της, την επανατοποθετούμε στο κουτί και στη συνέχεια επαναλαμβάνουμε τη διαδικασία άλλη μια φορά.
α) Να προσδιοριστεί ο δειγματικός χώρος του πειράματος τύχης.
β) Να προσδιοριστούν τα ενδεχόμενα.
- Α. Οι δύο μπάλες έχουν τον ίδιο αριθμό.
- Β. Ο αριθμός της πρώτης μπάλας είναι μεγαλύτερος από τον αριθμό της δεύτερης μπάλας.
- Γ. Ο αριθμός μιας μόνο μπάλας είναι 3.
Λύση
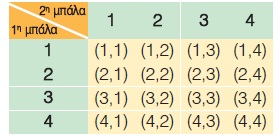
α) Ο δειγματικός χώρος του πειράματος αποτελείται από τα 16 στοιχεία του παρακάτω πίνακα, οπότε είναι:
Ω = {(1, 1), (1, 2), (1, 3), …, (4, 3) (4, 4)}.
β) Το ενδεχόμενο Α έχει ως στοιχεία εκείνα τα ζεύγη του Ω στα οποία ο πρώτος αριθμός είναι ίδιος με τον δεύτερο.
Άρα: Α = {(1, 1), (2, 2), (3, 3), (4, 4)}.
Το ενδεχόμενο Β έχει ως στοιχεία εκείνα τα ζεύγη του Ω στα οποία ο πρώτος αριθμός είναι μεγαλύτερος από τον δεύτερο.
Άρα: Β = {(2, 1) (3, 1), (3, 2), (4, 1), (4, 2) (4, 3)}.
Το ενδεχόμενο Γ έχει ως στοιχεία εκείνα τα ζεύγη του Ω στα οποία μόνο ένας από τους δύο αριθμούς είναι το 3.
Άρα: Γ = {(3, 1), (3, 2), (3, 4), (1, 3), (2, 3), (4, 3)}.
|
1
Ποια από τα παρακάτω είναι πειράματα τύχης:
α) Ρίχνω ένα ζάρι και καταγράφω την πάνω όψη του.
β) Αφήνω ένα βαρύ σώμα να πέσει και καταγράφω τη φορά της κίνησής του.
γ) Βγάζω ένα φύλλο από μία τράπουλα και σημειώνω ποιο είναι.
δ) Ανοίγω ένα βιβλίο και σημειώνω τον αριθμό που αντιστοιχεί στη δεξιά σελίδα του.
2
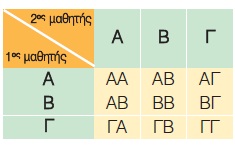
Επιλέγουμε διαδοχικά δύο μαθητές Γυμνασίου και καταγράφουμε την τάξη όπου φοιτούν. Ένας μαθητής για να βρει το δειγματικό χώρο έφτιαξε τον διπλανό πίνακα. Μήπως έκανε κάποιο λάθος;
3
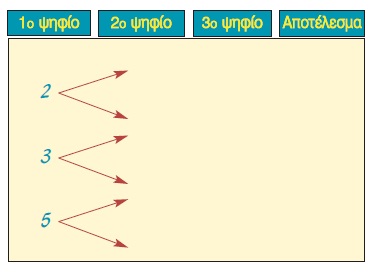
Το δεντροδιάγραμμα με το οποίο ένας μαθητής ήθελε να προσδιορίσει όλους τους τριψήφιους αριθμούς με ψηφία 2, 3, 5, που το καθένα χρησιμοποιείται μία μόνο φορά, έμεινε ημιτελές. Μπορείτε να το συμπληρώσετε;
4
Αν ο δειγματικός χώρος ενός πειράματος τύχης είναι Ω = {0, 2, 4, 6, 8, 10}, ποια από τα παρακάτω σύνολα είναι ενδεχόμενα του πειράματος;
α) Α = {4, 8, 10}
β) Β = {0, 2, 3, 6}
γ) Γ = {4, 7, 8, 10}
δ) Δ = {6}
5
Ρίχνουμε ένα ζάρι και φέρνουμε 6. Ποια από τα παρακάτω ενδεχόμενα πραγματοποιούνται:
α) Α = {2, 4, 6}
β) Β = {1, 3, 5}
γ) Γ = {4, 5, 6}
δ) Δ = {1, 2, 3}
6
Ένα κουτί περιέχει κόκκινες, κίτρινες και μαύρες μπίλιες. Αν επιλέξω μια μπίλια ποιο από τα παρακάτω ενδεχόμενα είναι αδύνατο;
α) Η μπίλια είναι κόκκινη.
β) Η μπίλια είναι κίτρινη.
γ) Η μπίλια είναι πράσινη.
δ) Η μπίλια δεν είναι μαύρη.
7
Επιλέγω στην τύχη ένα μήνα του έτους. Ποιο από τα παρακάτω ενδεχόμενα είναι βέβαιο;
α) Ο μήνας έχει 31 ημέρες.
β) Ο μήνας είναι θερινός.
γ) Το όνομα του μήνα αρχίζει από Μ.
δ) Ο μήνας έχει περισσότερες από 27 ημέρες. .
8
Να συμπληρώσετε τον παρακάτω πίνακα αντιστοιχίζοντας σε κάθε ενδεχόμενο της στήλης (Α) το σωστό συμπέρασμα από τη στήλη (Β).
| Στήλη Α |
Στήλη Β |
| α. |
Α U Β |
1. |
Δεν πραγματοποιείται το Α. |
| β. |
Α ∩ Β |
2. |
Πραγματοποιείται ένα τουλάχιστον από τα Α, Β. |
| γ. |
Α΄ |
3. |
Δεν πραγματοποιείται το Β. |
| |
|
4. |
Πραγματοποιούνται ταυτόχρονα και το Α και το Β |
|
|
|
1
Το κυλικείο ενός σχολείου διαθέτει για φαγητό σάντουιτς (σ), τυρόπιτα (τ), γλυκό (γ) και για αναψυκτικό πορτοκαλάδα (π), λεμονάδα (λ). Επιλέγουμε στην τύχη ένα μαθητή που αγόρασε ένα είδος φαγητού και ένα είδος αναψυκτικού και καταγράφουμε την προτίμησή του. Ποιος είναι ο δειγματικός χώρος του πειράματος;
2
Ρίχνουμε ένα νόμισμα τρεις φορές. Ποιος είναι ο δειγματικός χώρος του πειράματος;
3
Σ´ έναν προκριματικό όμιλο των Πανευρωπαϊκών αγώνων Μπάσκετ κληρώθηκαν να παίξουν τέσσερις ομάδες Α, Β, Γ, Δ δίνοντας μεταξύ τους από δύο αγώνες (εντός και εκτός έδρας). Με τη βοήθεια ενός πίνακα να βρείτε όλα τα ζεύγη των αντιπάλων.
4
Σ’ ένα κουτί υπάρχουν τρεις μπάλες, μία κόκκινη, μία άσπρη και μία μπλε που διαφέρουν μόνο ως προς το χρώμα. Επιλέγουμε τυχαία μια μπάλα και καταγράφουμε το χρώμα της.
α) Με πόσες το πολύ κινήσεις θα πάρουμε την κόκκινη μπάλα;
β) Με πόσες κινήσεις μπορούμε να αναγνωρίσουμε το χρώμα κάθε μπάλας;
γ) Θεωρείστε την πρώτη κίνηση ως ξεχωριστό πείραμα. Ποιος είναι ο δειγματικός του χώρος;
5
Σ´ ένα τηλεοπτικό παιχνίδι συμμετέχουν 4 άντρες (Δημήτρης, Κώστας, Μιχάλης, Παναγιώτης) και 3 γυναίκες (Ειρήνη, Ζωή, Σταματίνα). Επιλέγουμε στην τύχη έναν άντρα και μια γυναίκα για να διαγωνιστούν και καταγράφουμε τα ονόματα των αντιπάλων. Να προσδιορίσετε:
α) Το δειγματικό χώρο του πειράματος.
β) Τα ενδεχόμενα
- Α: διαγωνίστηκαν η Ειρήνη ή η Ζωή.
- Β: Δε διαγωνίστηκε ο Μιχάλης.
6
Ο δειγματικός χώρος ενός πειράματος τύχης είναι Ω = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Να παραστήσετε με διάγραμμα Venn τα ενδεχόμενα Α = { x ∈ Ω, όπου x διαιρέτης του 9} και Β = {x ∈ Ω, όπου x < 6} και να προσδιορίσετε το ενδεχόμενο που πραγματοποιείται, όταν:
α) Πραγματοποιείται ένα τουλάχιστον από τα Α, Β.
β) Πραγματοποιούνται ταυτόχρονα το Α και το Β.
γ) Δεν πραγματοποιείται το Β.
Μικροπείραμα 
7
Οι δράστες μια κλοπής διέφυγαν μ’ ένα αυτοκίνητο και μετά από την κατάθεση διαφόρων μαρτύρων έγινε γνωστό ότι ο τετραψήφιος αριθμός της πινακίδας του αυτοκινήτου είχε πρώτο και τέταρτο ψηφίο το 2. Το δεύτερο ψηφίο ήταν 6 ή 8 ή 9 και το τρίτο ψηφίο του ήταν 4 ή 7.
α) Ποιο είναι το σύνολο των πιθανών αριθμών της πινακίδας του αυτοκινήτου;
β) Να προσδιορίσετε τα ενδεχόμενα:
- Α:Το τρίτο ψηφίο του αριθμού της πινακίδας είναι το 7.
- Β:Το δεύτερο ψηφίο του αριθμού της πινακίδας είναι 6 ή 8.
|
|