- Μαθαίνω να σχεδιάζω τη γραφική παράσταση της συνάρτησης y = αx2 + βx + γ με α ≠ 0
Οι συναρτήσεις y = x2 και y = -x2, που γνωρίσαμε στην προηγούμενη παράγραφο, όπως και οι συναρτήσεις y = 3x2 - 1, y = -2x2 + 8x, y = x2 - 4x + 3 κ.τ.λ., ονομάζονται τετραγωνικές συναρτήσεις.
Γενικά
Τετραγωνική ονομάζεται κάθε συνάρτηση της μορφής y = αx2 + βx + γ με α ≠ 0.
Αν έχουμε μία τετραγωνική συνάρτηση, όπως την y = x2 - 4x + 3 και θέλουμε να σχεδιάσουμε τη γραφική της παράσταση, κατασκευάζουμε έναν πίνακα τιμών της για διάφορες τιμές του x.
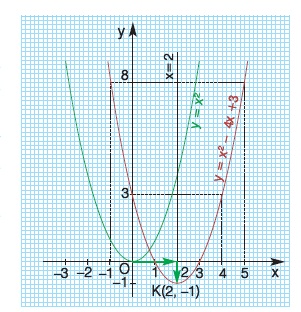
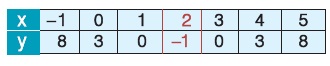
Σ' ένα σύστημα αξόνων παριστάνουμε με σημεία τα ζεύγη του προηγούμενου πίνακα και σχεδιάζουμε μια καμπύλη που διέρχεται από τα σημεία αυτά. Στο ίδιο σύστημα αξόνων σχεδιάζουμε την παραβολή y = x2, την αποτυπώνουμε σ' ένα διαφανές χαρτί και τη μετακινούμε οριζόντια προς τα δεξιά κατά 2 μονάδες και κατακόρυφα προς τα κάτω κατά 1 μονάδα. Διαπιστώνουμε ότι η παραβολή αυτή συμπίπτει με τη γραφική παράσταση της συνάρτησης y = x2 - 4x + 3.
Άρα η γραφική παράστασης της y = x2 - 4x + 3 είναι επίσης παραβολή, με κορυφή το σημείο Κ(2, -1) και άξονα συμμετρίας την κατακόρυφη ευθεία x = 2.
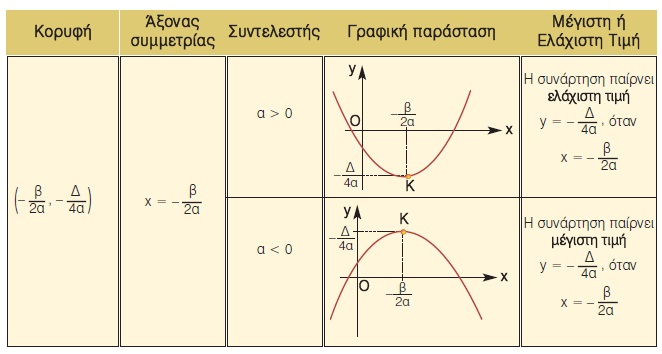
Γενικά
H γραφική παράσταση της συνάρτησης y = αx2 + βx + γ με α ≠ 0 είναι παραβολή με:
- Κορυφή το σημείο
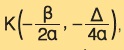 , όπου Δ = β2 - 4αγ και , όπου Δ = β2 - 4αγ και
- Άξονα συμμετρίας την κατακόρυφη ευθεία που διέρχεται από την κορυφή Κ και έχει εξίσωση
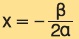
Στο προηγούμενο παράδειγμα από τον πίνακα τιμών και τη γραφική παράσταση διαπιστώσαμε ότι η παραβολή y = x2 - 4x + 3 έχει κορυφή το σημείο Κ(2, -1) και άξονα συμμετρίας την ευθεία x = 2. Στο ίδιο συμπέρασμα καταλήγουμε και από την προηγούμενη πρόταση,
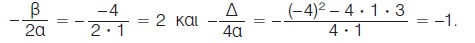
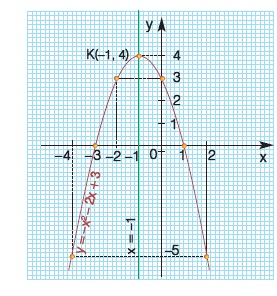 Ομοίως, η γραφική παράσταση της συνάρτησης y = -x2 - 2x + 3 είναι η παραβολή y = -x2 μετατοπισμένη παράλληλα προς τους άξονες, έχει κορυφή το σημείο Κ(-1, 4) και άξονα συμμετρίας την ευθεία x = -1, αφού Ομοίως, η γραφική παράσταση της συνάρτησης y = -x2 - 2x + 3 είναι η παραβολή y = -x2 μετατοπισμένη παράλληλα προς τους άξονες, έχει κορυφή το σημείο Κ(-1, 4) και άξονα συμμετρίας την ευθεία x = -1, αφού
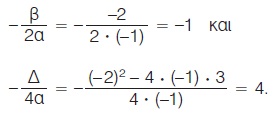
Από τις γραφικές παραστάσεις των συναρτήσεων y = x2 - 4x + 3 και y = -x2 -2x + 3, που σχεδιάσαμε στα προηγούμενα παραδείγματα, παρατηρούμε ακόμη ότι:
− Η συνάρτηση y = x2 - 4x + 3 που έχει α > 0 και γραφική παράσταση παραβολή με κορυφή το σημείο Κ(2, -1) παίρνει ελάχιστη τιμή y = -1, όταν x = 2.
− Η συνάρτηση y = -x2 - 2x + 3 που έχει α < 0 και γραφική παράσταση παραβολή με κορυφή το σημείο Κ(-1, 4) παίρνει μέγιστη τιμή y = 4, όταν x = -1.
Γενικά
- Αν α > 0, η συνάρτηση y = αx2 + βx + γ παίρνει ελάχιστη τιμή ,

- Αν α < 0, η συνάρτηση y = αx2 + βx + γ παίρνει μέγιστη τιμή ,

|
1
Να σχεδιαστεί η γραφική παράσταση της συνάρτησης y = x2 - 2 και να βρεθούν τα κοινά της σημεία με τον άξονα x΄x.
Λύση
H συνάρτηση y = x2 - 2 είναι της μορφής y = αx2 + βx + γ με α = 1, β = 0 και γ = -2, οπότε έχουμε
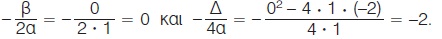
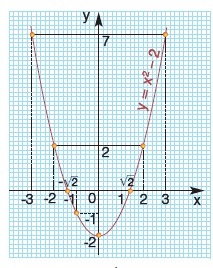
Άρα η γραφική της παράσταση είναι παραβολή με κορυφή το σημείο Κ(0, -2) και άξονα συμμετρίας την ευθεία x = 0, δηλαδή τον άξονα y΄y. Για τον ακριβέστερο σχεδιασμό της παραβολής προσδιορίζουμε μερικά ακόμη σημεία της.

Για να βρούμε τα κοινά σημεία της παραβολής y = x2 - 2 με τον άξονα x΄x θέτουμε y = 0 (τα σημεία του άξονα x΄x έχουν τεταγμένη 0) και έχουμε x2 - 2 = 0 ή x2 = 2, οπότε x =√2 ή x = -√2 . Άρα, τα κοινά σημεία της παραβολής και του άξονα x΄x είναι τα A( -√2 , 0) και B( √2, 0).
Παρατήρηση
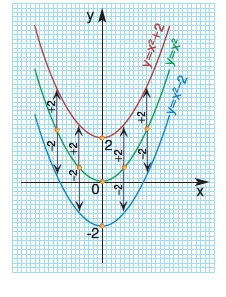
Η παραβολή y = x2 - 2, που έχει κορυφή το σημείο Κ(0, -2), μπορεί να προκύψει και με κατακόρυφη μετατόπιση της παραβολής y = x2 προς τα κάτω κατά 2 μονάδες (δεν υπάρχει οριζόντια μετατόπιση, γιατί η τετμημένη της κορυφής είναι 0).
Ομοίως, η παραβολή y = x2 + 2, που έχει κορυφή το σημείο Κ(0, 2) μπορεί να προκύψει και με κατακόρυφη μετατόπιση της παραβολής y = x2 προς τα πάνω κατά 2 μονάδες (δεν υπάρχει οριζόντια μετατόπιση, γιατί η τετμημένη της κορυφής είναι 0).
2
Να σχεδιαστεί η γραφική παράσταση της συνάρτησης y = (x - 2)2 και να βρεθεί το κοινό της σημείο με τον άξονα y΄y.
Λύση
H συνάρτηση y = (x - 2)2 γράφεται y = x2 - 4x + 4 και είναι της μορφής y = αx2+ βx+ γ με α = 1, β = -4 και γ = 4, οπότε έχουμε:
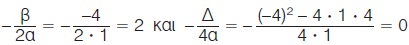
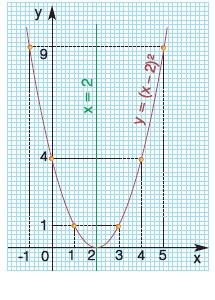
Άρα, η γραφική της παράσταση είναι παραβολή με κορυφή το σημείο Κ(2, 0) και άξονα συμμετρίας την ευθεία x = 2. Για τον ακριβέστερο σχεδιασμό της παραβολής προσδιορίζουμε μερικά ακόμη σημεία της.
Για να βρούμε το κοινό σημείο της παραβολής y = (x - 2)2 με τον άξονα y΄y, θέτουμε x = 0 (τα σημεία του άξονα y΄y έχουν τετμημένη 0), οπότε έχουμε y = (0 - 2)2 = 4. Άρα, το κοινό σημείο της παραβολής με τον άξονα y΄y είναι Α(0, 4).
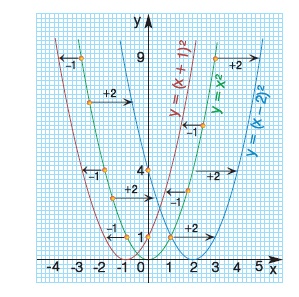
Παρατήρηση:
Η παραβολή y = (x - 2)2, που έχει κορυφή το σημείο Κ(2, 0), μπορεί να προκύψει και με οριζόντια μετατόπιση της παραβολής y = x2 προς τα δεξιά κατά 2 μονάδες (δεν υπάρχει κατακόρυφη μετατόπιση, γιατί η τεταγμένη της κορυφής είναι 0).
Ομοίως, η παραβολή y = (x + 1)2, που έχει κορυφή το σημείο Κ(-1, 0), μπορεί να προκύψει και με οριζόντια μετατόπιση της παραβολής y = x2 προς τα αριστερά κατά 1 μονάδα (δεν υπάρχει κατακόρυφη μετατόπιση, γιατί η τεταγμένη της κορυφής είναι 0).
Μικροπείραμα  Μικροπείραμα Μικροπείραμα 
3
Να σχεδιαστεί η γραφική παράσταση της συνάρτησης y = x2 - 4x και να προσδιοριστούν οι τιμές του x για τις οποίες είναι y < 0.
Λύση
H συνάρτηση y = x2 - 4x είναι της μορφής y = αx2 + βx + γ με α = 1, β = -4 και γ = 0, οπότε έχουμε
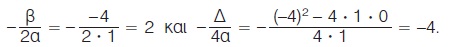
Άρα, η γραφική της παράσταση είναι παραβολή με κορυφή το σημείο Κ(2, -4) και άξονα συμμετρίας την ευθεία x = 2.
Για τον ακριβέστερο σχεδιασμό της παραβολής προσδιορίζουμε μερικά ακόμη σημεία της.
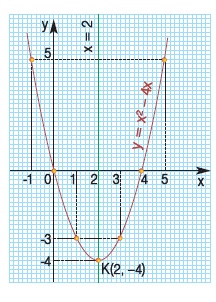

Σχεδιάζουμε την παραβολή και παρατηρούμε ότι τα σημεία της που έχουν τεταγμένη y αρνητική είναι εκείνα που έχουν τετμημένη x μεταξύ των αριθμών 0 και 4. Άρα, είναι y < 0, όταν 0 < x < 4.
|
1
Στο παρακάτω σχήμα δίνεται η γραφική παράσταση της συνάρτησης y = x2 - 2x - 3. Να συμπληρώσετε τα κενά σε καθεμιά από τις παρακάτω προτάσεις.
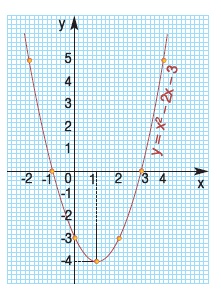
α) Η γραφική παράσταση είναι ………………… με κορυφή το σημείο ………… και άξονα συμμετρίας την ευθεία ………………
β) Η συνάρτηση αυτή παίρνει …………… τιμή y =…………… , όταν x = ………………
γ) Η γραφική παράσταση τέμνει τον άξονα x΄x στα σημεία ……………… , ………………… και τον άξονα y΄y στο σημείο………………. .
2
Να επιλέξετε τη σωστή απάντηση. Η παραβολή y = 4x2 + 2 έχει:
i) Κορυφή το σημείο
α) (4, 2)
β) (0, 4)
γ) (0, 2)
δ) (2, 0)
ii) Άξονα συμμετρίας την ευθεία με εξίσωση
α) x = 2
β) y = 0
γ) x = 0
δ) y = 2
5
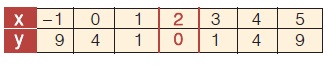
Ορισμένες τιμές της συνάρτησης y = αx2 + βx + γ με α < 0 φαίνονται στον πίνακα.

Να συμπληρώσετε τα κενά σε καθεμιά από τις παρακάτω προτάσεις:
α) Η γραφική παράσταση της συνάρτησης είναι παραβολή με άξονα συμμετρίας την ευθεία …………………… και κορυφή το σημείο …………
β) Η συνάρτηση αυτή παίρνει μέγιστη τιμή y = ……, όταν x = …………
γ) Η γραφική παράσταση της συνάρτησης τέμνει τον άξονα x΄x στα σημεία ……………… , ……………… και τον άξονα y΄y στο σημείο …………………
Μικροπείραμα 
|
1
Να σχεδιάσετε τις παραβολές:
α) y = x2 + 2x - 3 β) y = -2x2 + 4x + 6
2
Να βρείτε τη μέγιστη ή την ελάχιστη τιμή κάθε συνάρτησης:
α) y = 3x2 - 12x + 11 β) y = -4x2 -8x + 1 γ) y = -2(x - 6)2 + 7
Μικροπείραμα 
3
Να σχεδιάσετε τη γραφική παράσταση της συνάρτησης y = x2 + 2x για -4 ≤ x ≤2 και με τη βοήθεια αυτής να βρεθούν οι τιμές του x, για τις οποίες ισχύει x2 + 2x = 3.
4
Να σχεδιάσετε τη γραφική παράσταση της συνάρτησης y = x2 - 2x + 2 και με τη βοήθεια αυτής να αποδείξετε ότι x2 + 2 > 2x για κάθε πραγματικό αριθμό x.
5
Δίνεται η συνάρτηση y = x2 + 3x + λ.
α) Για ποια τιμή του πραγματικού αριθμού λ το σημείο Α(1, 6) ανήκει στη γραφική παράσταση της συνάρτησης;
β) Αν λ = 2, να σχεδιάσετε τη γραφική παράσταση της συνάρτησης για -4 ≤ x ≤ 1 και να βρείτε τα κοινά της σημεία με τους άξονες.
6
Να σχεδιάσετε την παραβολή y = x2 - 6x + 5. Αν Α, Β, Γ είναι τα κοινά της σημεία με τους άξονες, να υπολογίσετε το εμβαδόν του τριγώνου ΑΒΓ.
7
Να βρείτε τους αριθμούς β και γ, ώστε η συνάρτηση y = x2 + βx + γ για x = 4 να παίρνει ελάχιστη τιμή την y = -7.
8
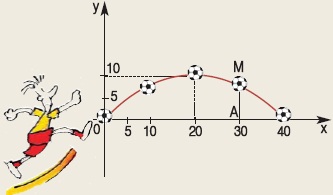
Ένας ποδοσφαιριστής έδιωξε την μπάλα από το σημείο Ο, η οποία αφού διέγραψε μια παραβολική τροχιά με μέγιστο ύψος 10 m έφτασε σε απόσταση 40 m.
α) Να αποδείξετε ότι η παραβολή έχει εξίσωση 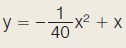 , με 0 ≤ x≤ 40. , με 0 ≤ x≤ 40.
β) Ποια ήταν η απόσταση της μπάλας από το έδαφος, όταν αυτή βρισκόταν στο σημείο Μ, που έχει τετμημένη 30 και σε ποιο άλλο σημείο της τροχιάς η μπάλα απείχε από το έδαφος την ίδια απόσταση;
Μικροπείραμα 
|
1
Στο ίδιο σύστημα αξόνων, να σχεδιάσετε τις δύο παραβολές, που οι συντεταγμένες των σημείων τους επαληθεύουν την εξίσωση 9y2 = 4x4.
2
Να βρείτε την τιμή του α, ώστε οι εξισώσεις y = (2α - 1)x2 και y = (1 - 4α2)x2 να παριστάνουν παραβολές συμμετρικές ως προς τον άξονα x΄x.
Μικροπείραμα 
3
Στο ίδιο σύστημα αξόνων να σχεδιάσετε τις γραφικές παραστάσεις των συναρτήσεων y = -x2, y = 2x - 3 και να προσδιορίσετε τις συντεταγμένες των κοινών τους σημείων.
Μικροπείραμα 
4
Να βρείτε την εξίσωση της παραβολής, που έχει κορυφή το σημείο Κ(2, -3) και τέμνει τον άξονα y΄y στο σημείο Α(0, 5).
5
Το άθροισμα των καθέτων πλευρών ενός ορθογωνίου τριγώνου ΑΒΓ ( Â = 90º) είναι 10 cm.
α) Να αποδείξετε ότι το εμβαδόν y του ορθογωνίου τριγώνου ως συνάρτηση της πλευράς του ΑΒ = x είναι 
β) Να σχεδιάσετε τη γραφική παράσταση της συνάρτησης.
γ) Να αποδείξετε ότι το εμβαδόν γίνεται μέγιστο, όταν το ορθογώνιο τρίγωνο είναι και ισοσκελές.
6
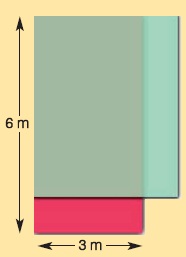
Ένα κατάστημα σχήματος ορθογωνίου αρχικά σχεδιάστηκε, να κατασκευαστεί με μήκος 6 m και πλάτος 3 m. Η αρχιτέκτων όμως, προκειμένου να μεγαλώσει τη βιτρίνα του καταστήματος σκέφτηκε να μειώσει το μήκος του και ταυτόχρονα να αυξήσει το πλάτος του 6 m κατά τα ίδια μέτρα. Ποια πρέπει να είναι η μεταβολή κάθε διάστασης, ώστε το εμβαδόν να γίνει μέγιστο;
Μικροπείραμα 
7
Σε ευθύγραμμο τμήμα ΑΒ = 10 cm παίρνουμε σημείο Μ και κατασκευάζουμε τα τετράγωνα ΑΜΓΔ και ΒΜΕΖ. Πού πρέπει να βρίσκεται το σημείο Μ, ώστε το άθροισμα των εμβαδών των δύο τετραγώνων να γίνει ελάχιστο;
8
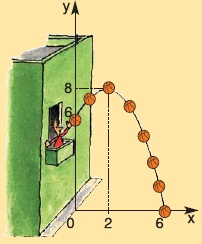
Από το μπαλκόνι ενός σπιτιού και από ύψος 6 m από το έδαφος πετάμε μία μπάλα, η οποία διαγράφει παραβολική τροχιά με μέγιστο ύψος από το έδαφος 8 m, όπως φαίνεται στο σχήμα. Αν η μπάλα προσκρούσει στο έδαφος σ' ένα σημείο που απέχει 6 m από το πεζοδρόμιο, τότε:
α) Να αποδείξετε ότι η εξίσωση της τροχιάς της μπάλας στο σύστημα αξόνων που φαίνεται στο σχήμα είναι 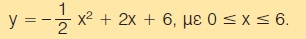
β) Ποια ήταν η απόσταση της μπάλας από το σημείο ρίψης όταν κατά την κάθοδο της βρισκόταν και πάλι σε ύψος 6 m από το έδαφος;
9
Στο παρακάτω σχήμα φαίνεται η κάθετη τομή μιας σήραγγας που κατασκευάστηκε σε σχήμα παραβολής με μέγιστο πλάτος ΑΒ = 16 m και μέγιστο ύψος ΟΓ = 6 m.
α) Να αποδείξετε ότι η εξίσωση της παραβολής στο σύστημα αξόνων του σχήματος είναι
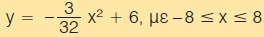
β) Ποιο είναι το μέγιστο ύψος ενός φορτηγού που μπορεί να διασχίσει τη σήραγγα, όταν το πλάτος του φορτηγού είναι 3,2 m και ο δρόμος είναι μιας κατεύθυνσης.
|
|
α) Η συνάρτηση y = αx2 με α ≠ 0
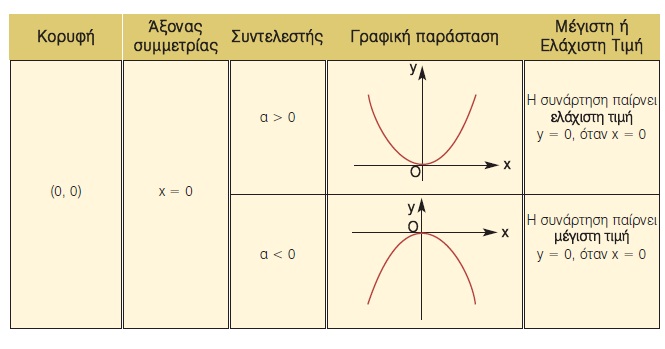
β) Η συνάρτηση y = αx2 + βx + γ με α ≠ 0
|
|