- Θυμάμαι πώς ορίζεται η διάταξη μεταξύ πραγματικών αριθμών.
- Μαθαίνω να αποδεικνύω και να χρησιμοποιώ τις ιδιότητες της διάταξης.
- Θυμάμαι πώς λύνονται οι ανισώσεις πρώτου βαθμού με έναν άγνωστο.
Γνωρίζουμε ότι κάθε πραγματικός αριθμός παριστάνεται με ένα σημείο ενός άξονα. Αν στον άξονα έχουμε δύο οποιουσδήποτε πραγματικούς αριθμούς, τότε μεγαλύτερος είναι εκείνος που βρίσκεται δεξιότερα
π.χ. -2 > -4, -3 < 2, π > √2

Δύο ή περισσότεροι πραγματικοί αριθμοί που έχουν παρασταθεί με σημεία ενός άξονα είναι διατεταγμένοι, οπότε μπορούμε να τους συγκρίνουμε.
Επομένως:
- Κάθε θετικός αριθμός είναι μεγαλύτερος από το μηδέν.
- Κάθε αρνητικός αριθμός είναι μικρότερος από το μηδέν.
- Κάθε θετικός αριθμός είναι μεγαλύτερος από κάθε αρνητικό αριθμό.
Πώς όμως θα συγκρίνουμε δύο οποιουσδήποτε πραγματικούς αριθμούς που δεν έχουν παρασταθεί με σημεία ενός άξονα;
Αν πάρουμε δύο αριθμούς, π.χ. τους 5 και 3, για τους οποίους ισχύει 5 > 3, παρατηρούμε ότι έχουν διαφορά ένα θετικό αριθμό, αφού 5 - 3 = 2 > 0.
Ομοίως, οι αριθμοί -2 και -4, για τους οποίους ισχύει -2 > -4, παρατηρούμε ότι έχουν διαφορά ένα θετικό αριθμό, αφού (-2) - (-4) = -2 + 4 = 2 > 0.
Αντίθετα, οι αριθμοί 3 και 5 ή -4 και -2, για τους οποίους ισχύει 3 < 5 και -4 < -2, παρατηρούμε ότι έχουν διαφορά έναν αρνητικό αριθμό, αφού 3 - 5 = - 2 < 0 και (-4) - (-2) = -4 + 2 = -2 < 0. Γενικά ισχύει:
Αν α > β τότε α - β > 0 ενώ Αν α < β τότε α - β < 0
Για να συγκρίνουμε λοιπόν δύο πραγματικούς αριθμούς α και β, που δεν έχουν παρασταθεί με σημεία ενός άξονα, βρίσκουμε τη διαφορά τους α - β και εξετάζουμε αν είναι θετική ή αρνητική ή μηδέν. |
- Αν α - β > 0 τότε α > β
- Αν α - β < 0 τότε α< β
- Αν α - β = 0 τότε α = β
|
O ορισμός της διάταξης μεταξύ πραγματικών αριθμών χρησιμοποιείται και για την απόδειξη των ιδιοτήτων της διάταξης. Οι ιδιότητες αυτές είναι:
α) Αν και στα δύο μέλη μιας ανισότητας προσθέσουμε ή αφαιρέσουμε τον ίδιο αριθμό, τότε προκύπτει ανισότητα με την ίδια φορά.
Π.χ. είναι 8 > 4, οπότε 8 + 3 > 4 + 3 και 8 - 3 > 4 - 3.
Γενικά ισχύει:
Αν α > β τότε α + γ > β + γ και α - γ > β - γ
Απόδειξη
- Για να συγκρίνουμε τους αριθμούς α + γ και β + γ, βρίσκουμε τη διαφορά τους και εξετάζουμε αν είναι θετική ή αρνητική ή μηδέν. Έτσι έχουμε:(α + γ) - (β + γ) = α + γ - β - γ = α - β. Είναι όμως α > β, οπότε α - β > 0. Δηλαδή η διαφορά (α + γ) - (β + γ) είναι θετικός αριθμός, οπότε α + γ > β + γ.
- Με ανάλογο τρόπο αποδεικνύουμε και α - γ > β - γ.
β) Αν πολλαπλασιάσουμε ή διαιρέσουμε και τα δύο μέλη μιας ανισότητας με τον ίδιο θετικό αριθμό, τότε προκύπτει ανισότητα με την ίδια φορά.
Π.χ. είναι 8 > 4, οπότε 8·2 > 4·2 και 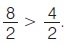 Γενικά ισχύει: Γενικά ισχύει:

Απόδειξη
- Για να συγκρίνουμε τους αριθμούς αγ και βγ, βρίσκουμε τη διαφορά τους και εξετάζουμε αν είναι θετική ή αρνητική ή μηδέν. Έτσι έχουμε αγ - βγ = γ(α - β) (1). Είναι όμως γ > 0 και α - β > 0, αφού α > β. Άρα οι αριθμοί γ και α - β είναι θετικοί, οπότε έχουν γινόμενο θετικό, δηλαδή γ(α - β) > 0. Από την ισότητα (1) έχουμε ότι η διαφορά αγ - βγ είναι θετικός αριθμός, οπότε αγ > βγ.
- Με ανάλογο τρόπο αποδεικνύουμε και
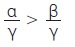
γ) Αν πολλαπλασιάσουμε ή διαιρέσουμε και τα δύο μέλη μιας ανισότητας με τον ίδιο αρνητικό αριθμό, τότε προκύπτει ανισότητα με αντίθετη φορά.
Π.χ. είναι 8 > 4, οπότε 8·(-2) <4·(-2) και -8- < -4. Γενικά αποδεικνύεται ότι:

δ) Αν προσθέσουμε κατά μέλη δύο ή περισσότερες ανισότητες που έχουν την ίδια φορά, τότε προκύπτει ανισότητα με την ίδια φορά.
Π.χ. είναι 3 > 2 και 7 > 4, οπότε 3 + 7 > 2 + 4.
Γενικά αποδεικνύεται ότι:
Αν α > β και γ > δ τότε α + γ > β + δ
Από τις προηγούμενες ιδιότητες προκύπτει και η μεταβατική ιδιότητα:
Αν α > β και β > γ τότε α > γ
Π.χ. είναι 3 > 1 και 1 > -2,5 οπότε 3 > -2,5.
ε) Αν πολλαπλασιάσουμε κατά μέλη δύο ή περισσότερες ανισότητες που έχουν την ίδια φορά και θετικά μέλη, τότε προκύπτει ανισότητα με την ίδια φορά.
Π.χ. είναι 3 > 2 > 0 και 7 > 4 > 0, οπότε 3·7 > 2·4. Γενικά ισχύει:
Αν α, β, γ, δ θετικοί πραγματικοί αριθμοί με α > β και γ > δ τότε αγ > βδ
Απόδειξη
Είναι α > β και γ > 0, οπότε σύμφωνα με την ιδιότητα (β) έχουμε αγ > βγ (1)
Είναι γ > δ και β > 0, οπότε για τον ίδιο λόγο έχουμε βγ > βδ (2)
Από τις ανισότητες (1), (2) και σύμφωνα με τη μεταβατική ιδιότητα έχουμε αγ > βδ.
Παρατηρήσεις:
1) Υπενθυμίζουμε ότι το τετράγωνο κάθε πραγματικού αριθμού α είναι μη αρνητικός αριθμός, δηλαδή ισχύει α2 ≥ 0Επομένως:
Αν για τους πραγματικούς αριθμούς α, β ισχύει α2 + β2 = 0, τότε α = 0 και β = 0.
2) Δεν επιτρέπεται να αφαιρούμε ή να διαιρούμε ανισότητες κατά μέλη, γιατί είναι δυνατό να οδηγηθούμε σε λανθασμένο συμπέρασμα. Πράγματι, αν αφαιρέσουμε ή διαιρέσουμε κατά μέλη τις ανισότητες 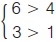 , τότε καταλήγουμε στις ανισότητες 3 > 3 ή 2 > 4, που δεν ισχύουν. , τότε καταλήγουμε στις ανισότητες 3 > 3 ή 2 > 4, που δεν ισχύουν.
Οι ιδιότητες της διάταξης χρησιμοποιούνται και για την επίλυση ανισώσεων. Για παράδειγμα, αν θέλουμε να επιλύσουμε την ανίσωση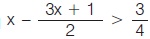 , που είναι πρώτου βαθμού με έναν άγνωστο, εργαζόμαστε ως εξής: , που είναι πρώτου βαθμού με έναν άγνωστο, εργαζόμαστε ως εξής:
Πολλαπλασιάζουμε και τα δύο μέλη της ανίσωσης με το Ε.Κ.Π. των παρονομαστών. (Στο παράδειγμα έχουμε Ε.Κ.Π. = 4> 0, οπότε η φορά της ανίσωσης δεν αλλάζει, ιδιότητα β),
Απαλείφουμε τους παρονομαστές.
Κάνουμε τις πράξεις και βγάζουμε τις παρενθέσεις
Χωρίζουμε γνωστούς από αγνώστους (προσθέτοντας και στα δύο μέλη τον ίδιο αριθμό, ιδιότητα α).
Κάνουμε αναγωγή ομοίων όρων.
Διαιρούμε και τα δύο μέλη της ανίσωσης με το συντελεστή του αγνώστου. (Στο παράδειγμα ο συντελεστής είναι -2 < 0 και γι´ αυτό αλλάζει η φορά της ανίσωσης, ιδιότητα γ).
Μικροπείραμα 
|
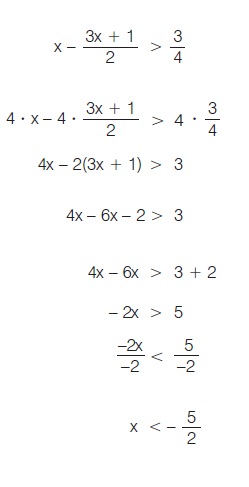 |
|
1
Ποιες ιδιότητες της διάταξης πρέπει να εφαρμόσουμε στην ανισότητα α > 4 για να αποδείξουμε τις παρακάτω ανισότητες;
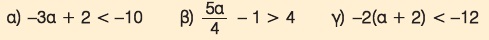
Λύση
| α) |
α > 4
-3α < -12
-3α + 2 < -12 + 2
-3α + 2 < -10
|
(πολλαπλασιάζουμε και τα δύο μέλη της ανισότητας με -3)
(προσθέτουμε και στα δύο μέλη της ανισότητας το 2) |
| β) |
 |
| γ) |
α > 4
α + 2 > 4 + 2
α + 2 > 6
-2(α + 2) <-2·6
-2(α + 2) < -12 |
(προσθέτουμε και στα δυο μέλη της ανίσωσης το 2)
(πολλαπλασιάζουμε και τα δυο μέλη της ανίσωσης με το -2) |
2
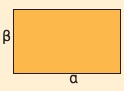
Για τις διαστάσεις α, β ενός ορθογωνίου ισχύουν 4 ≤ α≤ 6 και 2,5 ≤ β≤ 4,5.
Ποιες τιμές μπορεί να πάρει
α) η περίμετρος του ορθογωνίου;
β) το εμβαδόν του ορθογωνίου;
Λύση
3
Για οποιουσδήποτε πραγματικούς αριθμούς x, y, να αποδειχτεί ότι ισχύει x2 + y2≥ 2xy. Πότε ισχύει η ισότητα;
Λύση
Για να αποδείξουμε ότι x2 + y2 ≥ 2xy, αρκεί να αποδείξουμε ότι η διαφορά τους είναι μεγαλύτερη ή ίση του μηδενός, δηλαδή x2 + y2 - 2xy ≥ 0 ή (x - y)2 ≥ 0. H τελευταία σχέση είναι αληθής, αφού το τετράγωνο κάθε αριθμού είναι μη αρνητικός αριθμός. Η ισότητα ισχύει όταν (x - y)2 = 0, οπότε x - y = 0 δηλαδή x = y.
4
Οι μαθητές μιας τάξης προκειμένου να πάνε μια εκδρομή ζήτησαν προσφορά από δύο πρακτορεία.
− Το πρώτο πρακτορείο ζήτησε 15 ευρώ για κάθε μαθητή και εφόσον οι μαθητές ήταν πάνω από 25 θα έκανε και έκπτωση 10%.
− Το δεύτερο πρακτορείο ζήτησε 12 ευρώ για κάθε μαθητή και 45 ευρώ για τα διάφορα έξοδα (διόδια, ναύλα φεριμπότ κ.τ.λ.)
Αν οι μαθητές που συμμετέχουν στην εκδρομή είναι περισσότεροι από 25, ποιο πρακτορείο έκανε την καλύτερη προσφορά;
Λύση
Υποθέτουμε ότι οι μαθητές που τελικά συμμετέχουν στην εκδρομή είναι x, όπου x > 25.
Στο πρώτο πρακτορείο πρέπει να πληρώσουν 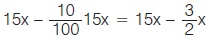 ευρώ, ενώ στο δεύτερο πρακτορείο πρέπει να πληρώσουν 12x + 45 ευρώ. Για να είναι καλύτερη η προσφορά του πρώτου πρακτορείου, πρέπει να ισχύει ευρώ, ενώ στο δεύτερο πρακτορείο πρέπει να πληρώσουν 12x + 45 ευρώ. Για να είναι καλύτερη η προσφορά του πρώτου πρακτορείου, πρέπει να ισχύει
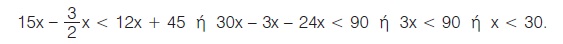
Επομένως αν οι μαθητές είναι περισσότεροι από 25 και λιγότεροι από 30, τότε την καλύτερη προσφορά έκανε το πρώτο πρακτορείο, ενώ αν οι μαθητές είναι περισσότεροι από 30, την καλύτερη προσφορά έκανε το δεύτερο πρακτορείο. Αν οι μαθητές είναι 30, τότε οι προσφορές των δύο πρακτορείων είναι ίδιες.
|
2
Να συμπληρώσετε τα κενά μ´ ένα από τα σύμβολα >, <, ≥, ≤, ώστε να προκύψουν αληθείς προτάσεις.
α) Αν α > 3, τότε α - 3 ... 0
β) Αν α < β και β < γ, τότε α ... γ
γ) Αν α > 0 και β < 0, τότε $\dfrac{α}{β}$ ... 0
δ) Αν γ< 0 και αγ < βγ, τότε α ... β
ε) Αν α ≠ 0, τότε α2 ... 0
στ) Αν α ≤ 0 και β ≤ 0, τότε α + β ... 0
3
Ποιες ιδιότητες της διάταξης χρησιμοποιούμε, ώστε από την ανίσωση 3x - 4 < 7 να γράψουμε 3x < 7 + 4 και από την ανίσωση 3x < 11 να γράψουμε 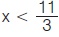 ; ;
4
Με ποιες ιδιότητες της διάταξης από την ανισότητα x > 3 προκύπτουν οι παρακάτω ανισότητες;
α) x + 4 > 7
β) x - 2 > 1
γ) 5x > 15
δ) -6x < -18
5
Αν α > 12 και β > 3, τότε ποιες από τις παρακάτω ανισότητες προκύπτουν από τις ιδιότητες της διάταξης;
α) α + β > 15
β) α - β > 9
γ) αβ > 36
δ) 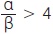
6
Ένας μαθητής γνωρίζει ότι για να είναι 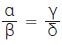 , αρκεί να ισχύει αδ = βγ. Βασιζόμενος σ´ αυτό σκέφτηκε ότι για να ισχύει , αρκεί να ισχύει αδ = βγ. Βασιζόμενος σ´ αυτό σκέφτηκε ότι για να ισχύει 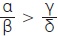 αρκεί να αποδείξει ότι αδ > βγ. Η σκέψη που έκανε είναι σωστή; αρκεί να αποδείξει ότι αδ > βγ. Η σκέψη που έκανε είναι σωστή;
|
1
Αν ισχύει 3(α - β) > 2(α + β), τότε να αποδείξετε ότι α > 5β.
2
Ποιες ιδιότητες της διάταξης πρέπει να εφαρμόσου-με στην ανισότητα x > -6 για να αποδείξουμε τις παρακάτω ανισότητες;
α) -5x - 30 < 0
β) 3x + 18 > 0
γ) 2(x + 4) > - 4
3
Αν 2 < α < 6, να βρείτε μεταξύ ποιών αριθμών βρίσκονται οι αριθμοί
α) α - 2
β) 2α - 5
γ) 1 - 3α
4
Αν α< β, τότε να αποδείξετε ότι

5
Αν 1 < x < 3 και 2< y < 5, να αποδείξετε ότι:
α) 3 < x + y < 8
β) 4 < 2x + y < 11
γ) -4 < x - y < 1
6
Αν x > 2 και y > 3, τότε να αποδείξετε ότι:
α) xy > 6
β) (x - 2)(y - 3) > 0
γ) (x + 2)y > 12
7
Αν α, β θετικοί αριθμοί με α > β, τότε να αποδείξετε ότι α2 > β2
8
Να αποδείξετε ότι:
α) Αν α > 1, τότε α2 > α
β) Αν x > 2, τότε x3 > 2x2
9
Αν α > β και α, β ομόσημοι, τότε να αποδείξετε ότι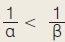
10
Αν x > 3 και y < 2, τότε να αποδείξετε ότι:
α) (x - 3)(y - 2) <0
β) xy + 6 < 2x + 3y
11
Για οποιουσδήποτε πραγματικούς αριθμούς x, y, να αποδείξετε ότι:
α) x2 + 1 ≥ 2x
β) (x + y)2 ≥ 4xy
γ) x2 + y2 + 1 ≥ 2y
Σε κάθε περίπτωση να βρείτε πότε ισχύει η ισότητα
12
Να αποδείξετε ότι:
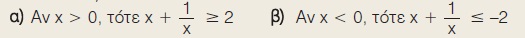
13
Να βρείτε το φυσικό αριθμό που είναι μεταξύ των αριθμών 114 και 135 και ο οποίος, όταν διαιρεθεί με το 15, δίνει υπόλοιπο 6.
14
Η τιμή ενός παντελονιού κυμαίνεται από 30 έως 35 € και μιας μπλούζας από 22 έως 25 €. Αν κάποιος θέλει ν´ αγοράσει 2 παντελόνια και 3 μπλούζες, τότε μεταξύ ποιων ποσών θα κυμαίνονται τα χρήματα που πρέπει να πληρώσει;
15

Μ´ ένα πούλμαν ταξιδεύουν 51 άτομα (ο οδηγός και 50 επιβάτες). Αν το βάρος κάθε ατόμου κυμαίνεται μεταξύ 60 kg και 100 kg, οι αποσκευές κάθε επιβάτη ζυγίζουν από 4 kg έως και 15 kg και το πούλμαν έχει απόβαρο 13,25 t, τότε να εκτιμήσετε το συνολικό βάρος του πούλμαν. Είναι δυνατόν το πούλμαν να διασχίσει μια γέφυρα επαρχιακού δρόμου που το ανώτατο επιτρεπόμενο βάρος διέλευσης είναι 20 t;
17
Να βρείτε τις κοινές λύσεις των ανισώσεων:
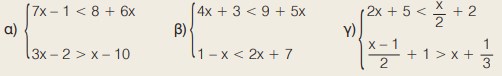
18
Να βρείτε θετικό ακέραιο αριθμό x, ώστε 
|
1
Αν α ≠ β, να λύσετε τις εξισώσεις:

2
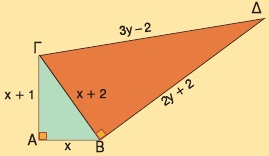
Στο παρακάτω σχήμα τα τρίγωνα ΑΒΓ και ΒΓΔ είναι ορθογώνια. Να βρείτε τις τιμές των x, y.
3
Το γινόμενο δύο θετικών διαδοχικών ακεραίων αριθμών, αν διαιρεθεί με το άθροισμά τους, δίνει πηλίκο 7 και υπόλοιπο 23. Να βρείτε τους αριθμούς.
4
Να λύσετε τις εξισώσεις, για τις διάφορες τιμές του α ≠ 0.
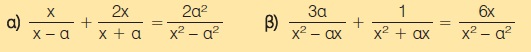
5
Αν μια λύση της εξίσωσης x2 + (λ - 5)x + λ = 0 είναι ο αριθμός 1, να βρείτε την άλλη λύση.
6
Δίνεται το πολυώνυμο Ρ(x) = x3 + 3x2 - 13x - 15. Να λύσετε την εξίσωση Ρ(x) = 0, αν είναι γνωστό ότι το x - 3 είναι παράγοντας του πολυωνύμου Ρ(x).
7
Να βρείτε δύο διαδοχικούς ακέραιους αριθμούς, τέτοιους ώστε το άθροισμα των αντιστρόφων τους αυξημένο κατά τον αντίστροφο του γινομένου τους να είναι ίσο με 1.
8
Να βρείτε τις διαστάσεις ενός οικοπέδου σχήματος ορθογωνίου, αν είναι γνωστό ότι οι πλευρές του διαφέρουν κατά 2 m και το εμβαδόν του οικοπέδου είναι 399 m2.
Μικροπείραμα 
9
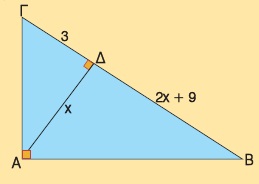
Δίνεται ορθογώνιο τρίγωνο ΑΒΓ (Â = 90º) και το ύψος του ΑΔ. Αν είναι ΑΔ = x, ΒΔ = 2x + 9 και ΓΔ = 3, να υπολογίσετε τον αριθμό x
Μικροπείραμα 
10
Να συγκρίνετε τους αριθμούς (1 + α)(1 + β) και 1 + α + β.
11
α) Να αποδείξετε ότι (α - β)2 + (β - γ)2 + (γ - α)2 = 2(α2 + β2 + γ2 - αβ - βγ - γα).
β) Αν για τους πραγματικούς αριθμούς α, β, γ ισχύει α2 + β2 + γ2 = αβ + βγ + γα, να αποδείξετε ότι α = β = γ.
12
Να αποδείξετε ότι 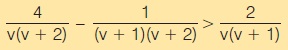 για κάθε θετικό ακέραιο ν. για κάθε θετικό ακέραιο ν.
13
Αν α, β, γ είναι τα μήκη των πλευρών τριγώνου, να αποδείξετε ότι:
α) α2 + β2 > γ2 - 2αβ
β) α2 + β2 < γ2 + 2αβ
γ) α2 + β2 + γ2 < 2αβ + 2βγ + 2αγ
14
Να διατάξετε τους θετικούς αριθμούς α, β, γ από το μικρότερο προς το μεγαλύτερο, αν ισχύει 2007α = 2008β = 2009γ.
15
Αν α > 4, να αποδείξετε ότι η εξίσωση (α + 1)x2 - (3α - 2)x + α + 1 = 0 έχει δύο λύσεις άνισες.
16
Να υπολογίσετε τους πραγματικούς αριθμούς α, β, γ που ικανοποιούν τη σχέση α2 + β2 + γ2 - 2α - 4β - 6γ + 14 = 0. (Διαγωνισμός Ε.Μ.Ε. 1995).
17
Να προσδιορίσετε την ελάχιστη τιμή της παράστασης Α = α2 - 10αβ + 27β2 - 8β + 8. Για ποιες τιμές των α, β η παράσταση Α γίνεται ελάχιστη; (Διαγωνισμός Ε.Μ.Ε. 2001).
19
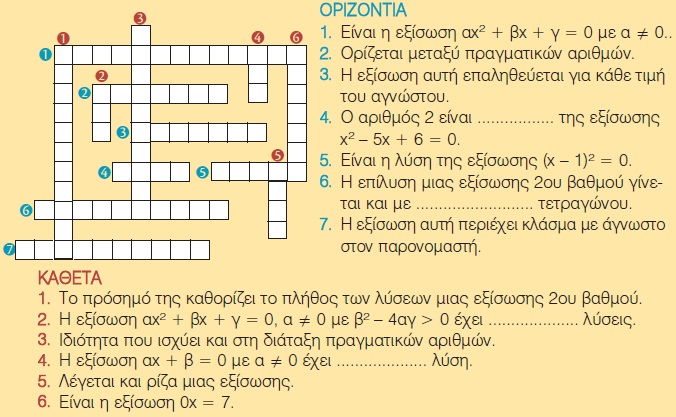
Να λύσετε το σταυρόλεξο
|
- Κλασματική εξίσωση ονομάζεται η εξίσωση που περιέχει ένα τουλάχιστον κλάσμα με άγνωστο στον παρονομαστή.
- Ένας αριθμός που μηδενίζει κάποιον παρονομαστή μιας κλασματικής εξίσωσης δεν μπορεί να είναι λύση (ή ρίζα) της.
| Ορισμός διάταξης: |
Αν α - β > 0, τότε α > β
Αν α - β < 0, τότε α< β
Αν α - β = 0, τότε α = β |
Ιδιότητες της διάταξης |
|
Παρατηρήσεις: |
- Για κάθε πραγματικό αριθμό α ισχύει α2≥ 0.
- Αν για τους πραγματικούς αριθμούς α, β ισχύει α2 + β2 = 0, τότε α = β = 0
- Δεν επιτρέπεται να αφαιρούμε ή να διαιρούμε ανισότητες κατά μέλη.
|
|