1.6 Παραγοντοποίηση αλγεβρικών παραστάσεων

Μαθαίνω να μετατρέπω μια αλγεβρική παράσταση σε γινόμενο παραγόντων

ΔΡΑΣΤΗΡΙΟΤΗΤΑ

1. Να γίνουν οι πράξεις:
2.. Σε μια κυκλική πλατεία ακτίνας R = 32,50 m κατασκευάστηκε ένα κυκλικό συντριβάνι ακτίνας ρ = 7,50 m. Να υπολογίσετε το εμβαδόν της πλατείας που απέμεινε μετά την κατασκευή του συντριβανιού.

Πολλές φορές, για την επίλυση ενός προβλήματος, μιας εξίσωσης, μιας ανίσωσης ή για την απλοποίηση ενός κλάσματος, είναι χρήσιμο να μετατραπεί μία παράσταση από άθροισμα σε γινόμενο.

Η διαδικασία με την οποία μια παράσταση, που είναι άθροισμα, μετατρέπεται σε γινόμενο παραγόντων, λέγεται παραγοντοποίηση.

Μικροπείραμα

Για παράδειγμα, η παράσταση πR² - πρ² με τη βοήθεια της επιμεριστικής ιδιότητας γράφεται π(R² - ρ²) και σύμφωνα με την ταυτότητα (R + ρ)(R - ρ) = R² - ρ², παραγοντοποιείται ως εξής:

πR² - πρ² = π(R² - ρ²) = π(R + ρ)(R- ρ)

Στο προηγούμενο παράδειγμα η παράσταση πR² – πρ² πήρε τελικά τη μορφή π(R + ρ) (R – ρ). Κανένας από τους παράγοντες π , (R + ρ) , (R - ρ) δεν μπορεί να μετατραπεί σε γινόμενο απλούστερων παραγόντων, γι´ αυτό λέμε ότι η παράσταση έχει αναλυθεί σε γινόμενο πρώτων παραγόντων.

Στο εξής, όταν λέμε ότι παραγοντοποιούμε μία παράσταση, θα εννοούμε ότι την αναλύουμε σε γινόμενο πρώτων παραγόντων.

Στη συνέχεια, θα δούμε τις πιο χαρακτηριστικές περιπτώσεις παραγοντοποίησης μιας αλγεβρικής παράστασης.

α) Κοινός παράγοντας

Αν όλοι οι όροι μιας παράστασης έχουν κοινό παράγοντα, τότε η παράσταση μετατρέπεται σε γινόμενο παραγόντων σύμφωνα με την επιμεριστική ιδιότητα.

Για παράδειγμα, σε όλους τους όρους της παράστασης 3α + 3β - 3γ υπάρχει κοινός παράγοντας το 3, οπότε η παράσταση παραγοντοποιείται ως εξής:

3α + 3β - 3γ = 3(α + β - γ).

Ομοίως η παράσταση 2α² - 2αβ + 2α, γράφεται 2α·α - 2α·β + 2α ·1, οπότε σε όλους τους όρους της υπάρχει κοινός παράγοντας το 2α.

Κάθε όρος μέσα στην παρένθεση είναι το πηλίκο της διαίρεσης των αντίστοιχων όρων της παράστασης με τον κοινό παράγοντα:

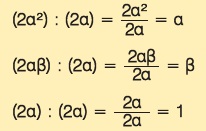
εικόνα

Άρα, η παράσταση παραγοντοποιείται ως εξής:

2α² - 2αβ + 2α = 2α(α - β + 1).

Στην περίπτωση αυτή, λέμε ότι «βγάζουμε κοινό παράγοντα το 2α».

Μικροπείραμα

Παραδείγματα

Να παραγοντοποιηθούν οι παραστάσεις:

α) 12x²y - 30xy² + 6x²y²

β) α(ω - x) + 3β(x - ω)

γ) 3(2x - 1) + x(4x - 2)

Λύση

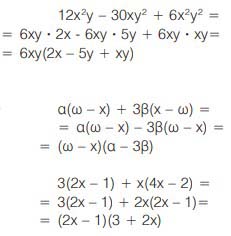
α) Σε όλους τους όρους της παράστασης υπάρχει κοινός παράγοντας το 6xy,οπότε έχουμε:

β) Η παράσταση έχει δύο όρους, τους α(ω - x) και 3, (x - ω). Για να δημιουργήσουμε και στους δύο όρους κοινό παράγοντα τον ω - x, το δεύτερο όρο της τον γράφουμε -3β(ω - x), οπότε έχουμε:

γ) Αν από το δεύτερο όρο της παράστασης βγάλουμε κοινό παράγοντα το 2, τότε δημιουργούμε κοινό παράγοντα το 2x - 1, οπότε έχουμε:

β) Κοινός παράγοντας κατά ομάδες (Ομαδοποίηση)

Στην παράσταση αx + αy + 2x + 2y, δεν υπάρχει κοινός παράγοντας σε όλους τους όρους της. Αν όμως βγάλουμε κοινό παράγοντα, από τους δύο πρώτους όρους το α και από τους δύο τελευταίους το 2, τότε σχηματίζονται δύο όροι με κοινό παράγοντα τον x + y. Έτσι, η παράσταση παραγοντοποιείται ως εξής:

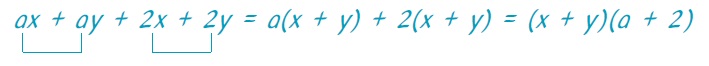
εικόνα

Την προηγούμενη παράσταση μπορούμε να τη χωρίσουμε και σε διαφορετικές ομάδες. Το αποτέλεσμα όμως της παραγοντοποίησης είναι και πάλι το ίδιο. Πράγματι, έχουμε:

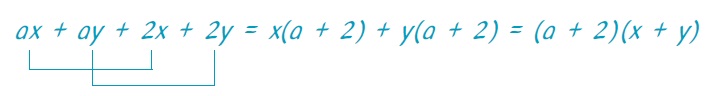
εικόνα

Παραδείγματα

Να παραγοντοποιηθούν οι παραστάσεις:

α) 3x³ - 12x² + 5x - 20

β) αβ - 3α - 3β + 9

γ) 3x² + 5xy + 2y²

Λύση

α) 3x³ - 12x² + 5x - 20 = 3x²(x - 4) + 5(x - 4) = (x - 4)(3x² + 5)

Μερικές παραστάσεις παραγοντοποιούνται κατά ομάδες, αν διασπάσουμε κατάλληλα έναν ή περισσότερους όρους π.χ.

5xy = 3xy + 2xy

β) αβ - 3α - 3β + 9 = α(β - 3) - 3(β - 3) = (β - 3)(α - 3)

γ) 3x² + 5xy + 2y² = 3x² + 3xy + 2xy + 2y² = 3x(x + y) + 2y(x + y) = (x + y)(3x + 2y).

γ) Διαφορά τετραγώνων

Αν εναλλάξουμε τα μέλη της ταυτότητας (α + β)(α - β) = α² - β², τότε γράφεται και ως εξής:

α² - β² = (α + β)(α - β)

Σύμφωνα με την ταυτότητα αυτή, μπορούμε να παραγοντοποιήσουμε μια παράσταση που είναι διαφορά τετραγώνων, π.χ. α² - 9 = α² - 3² = (α + 3)(α - 3).

Παραδείγματα

Να παραγοντοποιηθούν οι παραστάσεις:

α) 4β² - 25

β) (3x - 1)² - 81

γ) α² - 7.

Λύση

Για να σχηματίσουμε διαφορά τετραγώνων εκφράζουμε κάθε όρο ως τετράγωνο μιας παράστασης.

α) 4β² - 25 = (2β)² - 5² = (2β + 5)(2β - 5)

β) (3x - 1)² - 81 = (3x - 1)² - 9² =

(3x - 1 + 9)(3x - 1 - 9) =

(3x + 8)(3x - 10)

γ) α² -7 = α² -(√7 )² = (α - √7 )(α + √7 )

δ) Διαφορά - άθροισμα κύβων

Οι ταυτότητες (α - β)(α² + αβ + β²) = α³ - β³ και (α + β)(α² - αβ + β²) = α³+ β³ γράφονται και ως εξής:

α³ - β³ = (α - β)(α² + αβ + β²) α³ + β³ = (α + β)(α² - αβ + β²)

Σύμφωνα με τις ταυτότητες αυτές, μπορούμε να παραγοντοποιήσουμε μια παράσταση που είναι διαφορά ή άθροισμα κύβων, π.χ.

x³ - 64 = x³ - 4³ = (x - 4)(x² + x·4 + 4²) = (x - 4)(x² + 4x + 16)

y³ +27 = y³ + 3³ = (y + 3)(y² - y·3 + 3²) = (y + 3)(y² - 3y + 9)

Παραδείγματα

Να παραγοντοποιηθούν οι παραστάσεις:

α) x³ - 27

β) x³ + 64

γ) 8α³ - β³

Λύση

Για να σχηματίσουμε διαφορά ή άθροισμα κύβων εκφράζουμε κάθε όρο ως κύβο μιας παράστασης.

α) x³ - 27 = x³ - 3³ = (x - 3)(x² + x·3 + 3²) = (x - 3)(x² + 3x + 9)

β) x³ + 64 = x³ + 4³ = (x + 4)(x² - x·4 + 4²) = (x + 4)(x² - 4x + 16)

γ) 8α³ - β³ = (2α)³ - β³ = (2α - β)[(2α)² + 2α·β + β²] = (2α - β)(4α² + 2αβ + β²)

ε) Ανάπτυγμα τετραγώνου

Οι ταυτότητες (α + β)² = α² + 2αβ + β² και (α - β)² = α² - 2αβ + β² γράφονται και ως εξής:

α² + 2αβ + β² = (α + β)² α² - 2αβ + β² = (α - β)²

Σύμφωνα με τις ταυτότητες αυτές, μπορούμε να παραγοντοποιήσουμε μια παράσταση που είναι ανάπτυγμα τετραγώνου (τέλειο τετράγωνο), π.χ.

Οι παραστάσεις (x + 2)² και (y - 3)² είναι γινόμενα παραγόντων, αφού

(x + 2)² = (x + 2)(x + 2) και (y - 3)² = (y - 3)(y - 3)

x² + 4x + 4 = x² + 2·x·2 + 2² = (x + 2)²

y² - 6y + 9 = y² - 2·y·3 + 3² = (y - 3)²

Παραδείγματα

Να παραγοντοποιηθούν οι παραστάσεις:

α) 4α² + 12α + 9

β) α² - 10αβ + 25β²

γ) -4y² + 4y - 1

Λύση

Γράφουμε κάθε παράσταση ως ανάπτυγμα τετραγώνου της μορφής

α² + 2αβ + β² ή α² - 2αβ + β²

α) 4α² + 12α + 9 = (2α)² + 2·2α·3 + 3² = (2α + 3)²

β) α² - 10αβ + 25β² = α² - 2·α·5β + (5β)² = (α - 5β)²

γ) -4y² + 4y - 1 = -(4y² - 4y + 1) =
= -[(2y)² - 2·2y·1 + 1²] =
= -(2y - 1)²

στ) Παραγοντοποίηση τριωνύμου της μορφής x² + (α + β)x + αβ

Το ανάπτυγμα του γινομένου (x + α)(x + β) είναι το τριώνυμο x² + (α + β)x + αβ, αφού

(x + α)(x + β) = x² + αx + βx + αβ = x²+ (α + β)x + αβ.

Επομένως, ένα τριώνυμο της μορφής x² + (α + β)x + αβ

παραγοντοποιείται σύμφωνα με τον τύπο x² + (α + β)x + αβ = (x + α)(x + β)

Για παράδειγμα, για να παραγοντοποιήσουμε το τριώνυμο x² + 8x + 12 αναζητούμε δύο αριθμούς με γινόμενο 12 (σταθερός όρος) και άθροισμα 8 (συντελεστής του x). Υπάρχουν πολλά ζευγάρια αριθμών που έχουν γινόμενο 12 (π.χ. 1·12, 2·6, 3·4 κ.τ.λ.). Όμως, μόνο το ζευγάρι 2 και 6 έχει άθροισμα 8. Άρα έχουμε:

x² + 8x + 12 = x² + (6 + 2)x + 6·2 = (x + 6)(x + 2)

Μικροπείραμα

Παραδείγματα

Να παραγοντοποιηθούν τα τριώνυμα:

α) x²- 8x + 12

β) x² + 5x - 6

γ) -3y² + 12y - 9

Λύση

α) Για να παραγοντοποιήσουμε το τριώνυμο x²- 8x+12, αναζητούμε δύο αριθμούς με γινόμενο 12 και άθροισμα -8. Οι αριθμοί αυτοί πρέπει να είναι αρνητικοί, αφού έχουν γινόμενο θετικό και άθροισμα αρνητικό. Με δοκιμές βρίσκουμε ότι οι αριθμοί αυτοί είναι το -2 και το -6. Άρα έχουμε x² - 8x + 12 = (x - 2)(x - 6)

β) Για να παραγοντοποιήσουμε το τριώνυμο x² + 5x - 6, αναζητούμε δύο ετερόσημους αριθμούς, που έχουν γινόμενο -6 και άθροισμα 5. Οι αριθμοί αυτοί είναι το 6 και το -1, οπότε έχουμε x² + 5x - 6 = (x + 6)(x - 1).

γ) Για να παραγοντοποιήσουμε το τριώνυμο -3y² + 12y - 9, βγάζουμε κοινό παράγοντα το -3, ώστε ο συντελεστής του y² να γίνει 1, οπότε έχουμε -3y² + 12y - 9 = -3(y² - 4y + 3) Για την παραγοντοποίηση του τριωνύμου y² - 4y + 3, αναζητούμε δύο αριθμούς με γινόμενο 3 και άθροισμα -4. Οι αριθμοί αυτοί είναι το -3 και το -1, οπότε έχουμε -3y² + 12y - 9 = -3(y² - 4y + 3) = -3(y - 3)(y - 1).

ΠΑΡΑΔΕΙΓΜΑΤΑ − ΕΦΑΡΜΟΓΕΣ

α) Να παραγοντοποιηθεί η παράσταση 3x² - 18x.

β) Να λυθεί η εξίσωση 3x² = 18x.

Λύση

α) H παράσταση 3x² - 18x παραγοντοποιείται ως εξής: 3x² - 18x = 3x(x - 6).

β) Η εξίσωση 3x² = 18x γράφεται 3x² - 18x = 0 και σύμφωνα με το προηγούμενο ερώτημα έχουμε 3x(x - 6) = 0. Για να είναι το γινόμενο 3x(x - 6) ίσο με το μηδέν, πρέπει 3x = 0 ή x - 6 = 0, δηλαδή x = 0 ή x = 6.

Αν τοποθετήσουμε κατάλληλα τα τέσσερα σχήματα, σχηματίζουμε ένα ορθογώνιο. Να βρεθούν οι διαστάσεις του ορθογωνίου.

Λύση

α) Το ορθογώνιο που θα σχηματιστεί θα έχει εμβαδόν Ε, ίσο με το άθροισμα των εμβαδών των τεσσάρων σχημάτων, δηλαδή, Ε = x·1 + y·1 + xy + 1·1 = x + y + xy + 1. Όμως, x + y + xy + 1 = (x + xy) + (y + 1) = x = x(1 + y) + (1 + y) = (1 + y)(x + 1).

Άρα, οι διαστάσεις του ορθογωνίου είναι 1 + y και 1 + x.

Μικροπείραμα

Να υπολογιστούν οι αριθμητικές παραστάσεις χωρίς να χρησιμοποιηθεί υπολογιστής τσέπης:

α) 786·45 + 786·55

β) 2005² - 1995²

γ) 565·499 + 565·66 - 435².

Λύση

α) 786·45 + 786·55 = 786(45 + 55) = 786·100 = 78600

β) 2005² - 1995² =(2005 - 1995)(2005 + 1995) = 10·4000 = 40000

γ) 565·499 + 565·66 - 435² = 565(499 + 66) - 435² = 565² - 435² = (565 - 435)(565 + 435) = 130·1000 = 130000

Να αναλυθούν σε γινόμενο παραγόντων οι παραστάσεις:

α) 3x²y - 12y³ β) 5x²y + 10x² + 5xy + 10x

γ) x⁴- 16y⁴ δ) 16α³β - 54β

ε) x² - 4x + 4 - y² στ) 3x³ + 12x²- 15x

Λύση

α) 3x²y - 12y³ = 3y(x² - 4y²) = 3y [x² - (2y)²] = 3y(x - 2y)(x + 2y)

β) 5x²y + 10x² + 5xy + 10x = 5x(xy + 2x + y + 2) = 5x[y(x + 1) + 2(x + 1)] = 5x(x + 1)(y + 2)

γ) x⁴ - 16y⁴ = (x²)² - (4y²)² = (x² + 4y²)(x² - 4y²) = (x² + 4y²) [x² - (2y)²] = (x² + 4y²)(x - 2y)(x + 2y)

δ) 16α³β - 54β = 2β(8α³ - 27) = 2β[(2α)³ - 3³] = 2β(2α - 3)(4α² + 6α + 9)

ε) x²- 4x + 4 - y² = (x² - 2·x·2 + 2²) - y² = (x - 2)² - y² = (x - 2 + y)(x - 2 - y).

στ) 3x³ + 12x² - 15x = 3x(x² + 4x - 5)

To τριώνυμο x² + 4x - 5 παραγοντοποιείται, εφόσον υπάρχουν αριθμοί με γινόμενο -5 και άθροισμα 4, που είναι οι 5 και -1. Άρα, 3x² + 12x² - 15x = 3x(x² + 4x - 5) = 3x(x + 5)(x - 1).

ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ

Ποιες από τις παρακάτω παραστάσεις είναι γινόμενο παραγόντων;

α) 2(x - y)(x + y) β) 2 + (x - y)(x + y) γ) 4(α - β)²

δ) 4 + (α - β)² ε) (x + 2y)x - y στ) (x + 2y)(x - y) ζ) (α + β)(α + 3β)

η) (α + β)(α + 3β) + 1.

Να συμπληρώσετε τα κενά στις παρακάτω ισότητες.

α) 8x + 16 = 8(………) β) 3αy- y² = y(………) γ) 6x² + 12x = ……… (x + 2)

δ) -4x² + 8x = -4x(………) ε)√2x + √2 = √2 (………) στ) (x - 1)² - (x - 1) = (x - 1)(……)

Να επιλέξετε τη σωστή απάντηση. Η παράσταση 3x³ + 3x² + x + 1 παραγοντοποιείται ως εξής:

α) 3x²(x + 1) β) (x + 3)(3x² -1)

γ) (x + 1)(3x² + 1) δ) x(3x² + x + 1).

Να χαρακτηρίσετε τις παρακάτω προτάσεις με (Σ), αν είναι σωστές ή με (Λ), αν είναι λανθασμένες:

α) x² - 2² = (x - 2)(x + 2)
β) x² - 9 = (x - 9)(x + 9)
γ) 112² - 12² = 100·124
δ) 4y² - 1 = (4y - 1)(4y + 1)
ε) 4 x ² - α ² = (2 x - α)(2 x + α)
στ) α² - (β - 1)² = (α + β - 1)(α - β - 1)

Αν ισχυριστούμε ότι το εμβαδόν του πράσινου μέρους είναι (x - y)(x + y), αυτό είναι σωστό ή λάθος; Να αιτιολογήσετε την απάντησή σας.

Να συμπληρώσετε τα κενά στις παρακάτω ισότητες.

α) α³ - 2³ = (α - 2)(…………)

β) α³+ 3³ = (α + 3)(…………)

γ) (2x)³ - 1 = (2x - 1)(…………)

δ) 1 + (5y)³ = (1 + 5y)(…….…)

Να χαρακτηρίσετε τις παρακάτω ισότητες με (Σ), αν είναι σωστές ή με (Λ), αν είναι λανθασμένες.

α) x³ - 5³ = (x - 5)(x² - 5x + 25)
β) 8 + α³ = (2 + α)(2² - 2α + α²)
γ) (3y)³ + 1 = (3y + 1)(3y² - 3y + 1)
δ) 1 - (2β)³ = (1 - 2β)(1 + 2β + 4β³)

Να συμπληρώσετε τα κενά στις παρακάτω ισότητες.

α) x² + 6x + 9 = (……)²

β) 4α²- 4α + 1 = (.……)²

γ) y⁴ - 2y² + 1 = (……)²

δ) 25 + 10x³ + x⁶ = (……)²

Να επιλέξετε τη σωστή απάντηση.
Ο κύκλος εμβαδού πα² + 2πα + π, με α > 0, έχει ακτίνα

α) α + 2 β) α² + 1 γ) α + 1 δ) π(α + 1)

Να συμπληρώσετε τον πίνακα.

x² + (α + β)x + αβ	αβ	α + β	α	β	(x + α) (x + β)
x² + 3x + 2
x² - 3x + 2
x² + 5x - 6
x² + 5x + 6
x² - x - 2
x² + x - 2

Να συμπληρώσετε τα κενά στις παρακάτω ισότητες.

α ) x² + (α + 2)x + 2α = (x + ……)·(x + ……)

β) x² + ( √2 + √3 )x + √6 = (x + ……)·(x + ……)

ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ − ΠΡΟΒΛΗΜΑΤΑ

Να παραγοντοποιήσετε τις παραστάσεις:

α) 3α + 6β

β) 2x - 8

γ) 8ω² + 6ω

δ) -9x² - 6x

ε) 8α²β + 4αβ²

στ) 2x² - 2xy + 2x

ζ) α²β + αβ² - αβ

η) 2α³ - 4α² + 6α²β

θ) √2 xy - √18 y + √8 y²

Να παραγοντοποιήσετε τις παραστάσεις:

α) x(α - β) + y(α - β)

β) α(x + y) + β(x + y)

γ) (3x- 1)(x- 2) - (x + 4)(x - 2)

δ) α²(α - 2) - 3(2 - α)

ε) 4x(x - 1) - x + 1

στ) 2x²(x - 3) - 6x(x - 3)²

i) Να παραγοντοποιήσετε τις παραστάσεις:

α) x² + x
β) 2y² - 5y
γ) ω(ω - 3) - 2(3 - ω)
δ) α(3α + 1) - 4α

ii) Να επιλύσετε τις εξισώσεις:

α) x² + x = 0
β) 2y² = 5y
γ) ω(ω - 3) - 2(3 - ω) = 0
δ) α(3α + 1) = 4α

Να παραγοντοποιήσετε τις παραστάσεις:

α) x² + xy + αx + αy

β) x³ - x² + x - 1

γ) x³ - 5x² + 4x - 20

δ) 2x³ - 3x² + 4x - 6

ε) 4x² - 8x - αx + 2α

στ) 9αβ - 18β² + 10β - 5α

ζ) 12x² - 8xy - 15x + 10y

η) x³ + √2 x² + x +√2

θ) √6 x² + 2 √2 x - √3 x - 2

Να παραγοντοποιήσετε τις παραστάσεις:

α) 7α² + 10αβ + 3β²

β) 5x² - 8xy + 3y²

γ) 3x² - xy - 2y²

α) Να αναλύσετε σε γινόμενο παραγόντων την παράσταση α²β + αβ² - α - β.

β) Αν για τους αριθμούς α, β ισχύει α²β + αβ² = α + β, να αποδείξετε ότι οι αριθμοί α, β είναι αντίθετοι ή αντίστροφοι.

Να παραγοντοποιήσετε τις παραστάσεις:

α) 2α² - 2α + αβ - β + αx - x

β) 2αβ - 4β + 5α - 10 + 2αγ - 4γ

Να παραγοντοποιήσετε τις παραστάσεις:

α) x² - 9

β) 16x² - 1

γ) α² - 9β²

δ) α²β² - 4

ε) 36ω² - (ω + 5)²

στ) 4(x + 1)² - 9(x - 2)²

ζ) εικόνα

η) x² - 3

θ) x² - 2y²

Να παραγοντοποιήσετε τις παραστάσεις:

α) 2x² - 32

β) 28 - 7y²

γ) 2x³ - 2x

δ) 5αx² - 80α

ε) 2(x - 1)²− 8

εικόνα Στο ορθογώνιο τρίγωνο ΑΒΓ να υπολογίσετε την πλευρά γ, όταν:

α) α = 53, β = 28

β) α = 0,37, β = 0,12

γ) α = 26λ, β = 10λ

Να επιλύσετε τις εξισώσεις:

α) x² - 49 = 0

β) 9x³ - 4x = 0

γ) x(x + 1)² = 4x

δ) (x + 2)³ = x + 2

Να παραγοντοποιήσετε τις παραστάσεις:

α) x³ - 27

β) y³ + 8

γ) ω³ + 64

δ) 8x³ - 1

ε) 27y³ + 1

Να παραγοντοποιήσετε τις παραστάσεις:

α) 3x³ - 24

β) 16α⁴ + 2α

γ)

δ) α⁴β + αβ⁴

Να συμπληρώσετε τις ισότητες:

α) x³ - … = (x - 3)(… + … + 9)

β) … + y³ = (2x + y)(4x² - … + …)

γ) α³ - … = (α - 2β)(… + … + 4β²)

δ) α³ + … = (α + 5β)(… - … + 25β²)

Να παραγοντοποιήσετε τις παραστάσεις:

α) x² - 2x + 1

β) y² + 4y + 4

γ) ω² - 6ω + 9

δ) α² + 10α + 25

ε) 1 - 4β + 4β²

στ) 9x⁴ + 6x² + 1

ζ) 4y² - 12y + 9

η) 16x² + 8xy + y²

θ) 25α² - 10αβ + β²

ι) (α + β)² - 2(α + β) + 1

ια) - 2y +9

ιβ) x² + x +

Να παραγοντοποιήσετε τις παραστάσεις:

α) 3x² + 24x + 48

β) -y² + 4y - 4

γ) 2α² - 8αβ + 8β²

δ) 4α³ + 12α² + 9α

Να βρείτε:

α) Ένα πολυώνυμο που να εκφράζει το εμβαδόν του παρακάτω σχήματος.

β) Την πλευρά ενός τετραγώνου που έχει εμβαδόν ίσο με το εμβαδόν του διπλανού σχήματος.

Να βρείτε την πλευρά ενός τετραγώνου, που έχει εμβαδόν ίσο με το εμβαδόν του τετραπλεύρου ΑΒΓΔ.

Μικροπείραμα

Να παραγοντοποιήσετε τα τριώνυμα:

α) x² + 3x + 2

β) y² - 4y + 3

γ) ω² + 5ω + 6

δ) α² + 6α + 5

ε) x² - 7x + 12

στ) y² - y - 12

ζ) ω² - 9ω + 18

η) α² + 3α - 10

Να παραγοντοποιήσετε τα τριώνυμα:

α) x² + (2 +√3 )x + 2 √3

β) x² + (2α + 3β)x + 6αβ

γ) x² + (3 - √2 )x - 3√2

Να παραγοντοποιήσετε τις παραστάσεις:

α) 2ω² + 10ω + 8

β) 3α² - 12α - 15

γ) αx² - 7αx + 6α

Να υπολογίσετε τις αριθμητικές παραστάσεις χωρίς να χρησιμοποιήσετε υπολογιστή τσέπης.

α) 1453·1821 - 1453·821

β) 801² + 199·801

γ) 998² - 4

δ) 999·1001 + 1

ε) 999² + 2·999 + 1

στ) 97² + 6·97 + 9

Να παραγοντοποιήσετε τις παραστάσεις:

α) x²y² - 4y² - x² + 4

β) x⁴ - 1 + x³ - x

γ) x³(x² - 1) + 1 - x²

δ) (x² + 9)² - 36x²

ε) α² - 2αβ + β² - α + β

στ) x² - 2xy + y² - ω²

ζ) 1 - α² + 2αβ - β²

η) y² - x² - 10y + 25

θ) 2(x - 1)(x²- 4)-5(x - 1)(x - 2)²

ι) (y² - 4)² - (y + 2)²

ια) (α² + β² - γ²)² - 4α²β²

ιβ) (x² + 9)(α² + 4) - (αx + 6)²

Ενός ορθογωνίου οικοπέδου οι διαστάσεις x, y μειώθηκαν, επειδή έπρεπε να αυξηθεί το πλάτος των διπλανών δρόμων. Αν το εμβαδόν του οικοπέδου που απέμεινε είναι xy - x - 2y + 2, να βρείτε ποια θα μπορούσε να είναι η μείωση κάθε διάστασής του.