Μαθηματικά Γ΄ Γυμνασίου - Βιβλίο Μαθητή (εμπλουτισμένο)
1.5
Αξιοσημείωτες ταυτότητες
Εικόνα
Εικόνα
  • Θυμάμαι ποια ισότητα λέγεται ταυτότητα.
  • Γνωρίζω ποιες είναι οι βασικές ταυτότητες.
  • Μαθαίνω να αποδεικνύω μια απλή ταυτότητα.
ΔΡΑΣΤΗΡΙΟΤΗΤΑ
εικόνα
  • 1. Ποιες από τις ισότητες 3x = 12, x + y = 7, 4α = 3α + α, x(x + 2) = x2 + 2x, αληθεύουν για όλες τις τιμές των μεταβλητών τους;
  • 2.

    α) Να βρείτε το συνολικό εμβαδόν των πράσινων σχημάτων.

    β) Ποια από τις παρακάτω παραστάσεις εκφράζει το εμβαδόν του κίτρινου τετραγώνου;

    i) x2 + 9       ii) (x + 3)2

    iii) x2 + 6x       iv) 6x + 9

    γ) Να συγκρίνετε το συνολικό εμβαδόν των πράσινων σχημάτων με το εμβαδόν του κίτρινου τετραγώνου.

Υπάρχουν ισότητες που περιέχουν μεταβλητές και αληθεύουν για ορισμένες τιμές των μεταβλητών τους. Για παράδειγμα, η ισότητα 3x = 12, αληθεύει για x = 4 και δεν αληθεύει για καμιά άλλη τιμή του x. Ομοίως, η ισότητα x + y = 7, αληθεύει για x = 1 και y = 6, ή για x = 3 και y = 4, ενώ δεν αληθεύει για x = 4 και y = 5.

Υπάρχουν όμως και ισότητες, που αληθεύουν για όλες τις τιμές των μεταβλητών τους όπως για παράδειγμα οι ισότητες: α + β = β + α, 4α = 3α + α, x(x + 2) = x2 + 2x. Οι ισότητες αυτές λέγονται ταυτότητες.

Γενικά

Ταυτότητα λέγεται κάθε ισότητα που περιέχει μεταβλητές και αληθεύει για όλες τις τιμές των μεταβλητών της.

 

Ταυτότητες υπάρχουν πολλές, ορισμένες από αυτές τις συναντάμε πολύ συχνά και γι' αυτό αξίζει να τις θυμόμαστε. Αξιοσημείωτες ταυτότητες είναι:

α) Τετράγωνο αθροίσματος

Αν την παράσταση (α + β)2 τη γράψουμε (α + β)(α + β) και βρούμε το ανάπτυγμα του γινομένου, έχουμε:

(α + β)2 = (α + β)(α + β) =

= α2 + αβ + βα + β2 =

= α2 + 2αβ + β2

Αποδείξαμε λοιπόν την ταυτότητα (α + β)2 = α2 + 2αβ + β2

εικόνα

Το δεύτερο μέρος της προηγούμενης ισότητας λέγεται ανάπτυγμα του (α + β)2. Για παράδειγμα, το ανάπτυγμα του (y + 4)2 προκύπτει, αν στην προηγούμενη ταυτότητα αντικαταστήσουμε το α με το y και το β με το 4, οπότε έχουμε: (y + 4)2 = y2 + 2·y·4 + 42 = y2 + 8y + 16.

H προηγούμενη ταυτότητα, όπως και όλες οι επόμενες, χρησιμοποιούνται και όταν τα α, β είναι οποιεσδήποτε αλγεβρικές παραστάσεις, π.χ.

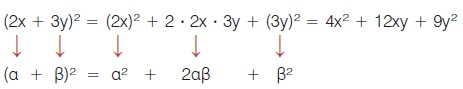
εικόνα

Μικροπείραμα μικροπείραμα    Μικροπείραμα μικροπείραμα    Μικροπείραμα μικροπείραμα

β) Τετράγωνο διαφοράς


Αν την παράσταση (α - β)2 τη γράψουμε (α - β)(α - β) και βρούμε το ανάπτυγμα του γινομένου, τότε μπορούμε να αποδείξουμε και την ταυτότητα

(α - β)2 = α2 - 2αβ + β2

Πράγματι έχουμε:
(α - β)2 = (α - β)(α - β) = α2 - αβ - βα + β2 = α2 - 2αβ + β2

Για παράδειγμα, το ανάπτυγμα του (y - 4)2 προκύπτει, αν αντικαταστήσουμε το α με το y και το β με το 4, οπότε έχουμε:

(y - 4)2 = y2 - 2· y·4 + 42 = y2 - 8y + 16 Ομοίως, για να υπολογίσουμε το ανάπτυγμα του (3x - 4y)2 έχουμε:

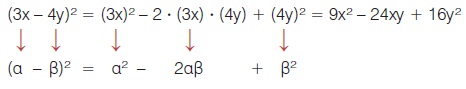
εικόνα

Μικροπείραμα μικροπείραμα    Μικροπείραμα μικροπείραμα

γ) Κύβος αθροίσματος - διαφοράς

Αν την παράσταση (α + β)3 τη γράψουμε (α + β)(α + β)2 και κάνουμε τον πολλαπλασιασμό του α + β με το ανάπτυγμα του (α + β)2, έχουμε:

(α + β)3 = (α + β)(α + β)2 =

= (α + β)(α2 + 2αβ + β2) =

= α3 + 2α2β + αβ2 + α2β + 2αβ2 + β3 =

= α3 + 3α2β + 3αβ2 + β3

Αποδείξαμε λοιπόν την ταυτότητα

(α + β)3 = α3 + 3α2β + 3αβ2 + β3

 

Με τον ίδιο τρόπο μπορούμε να αποδείξουμε και την ταυτότητα

(α - β)3 = α3 - 3α2β + 3αβ2 - β3

 

Σύμφωνα με τις προηγούμενες ταυτότητες έχουμε:

  • (x + 2)3 = x3 + 3·x2·2 + 3·x·22 + 23 = x3 + 6x2 + 12x + 8
  • (2x - 5)3 = (2x)3 - 3·(2x)2·5 + 3·(2x)·52 - 53 = 8x3 - 60x2 + 150x - 125.
δ) Γινόμενο αθροίσματος επί διαφορά

Αν βρούμε το ανάπτυγμα του γινομένου (α + β)(α - β) έχουμε:

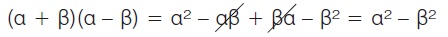
εικόνα

Αποδείξαμε λοιπόν την ταυτότητα

(α + β)(α - β) = α2 - β2

Η προηγούμενη ταυτότητα χρησιμοποιείται για να βρίσκουμε γρήγορα το γινόμενο αθροίσματος δύο παραστάσεων επί τη διαφορά τους. Για παράδειγμα, έχουμε:

  • (x + 2)(x - 2) = x2 - 22 = x2 - 4
  • (3α + 2β)(3α - 2β) = (3α)2 - (2β)2 = 9α2 - 4β2

Μικροπείραμα μικροπείραμα    Μικροπείραμα μικροπείραμα    Μικροπείραμα μικροπείραμα

ε) Διαφορά κύβων - Άθροισμα κύβων

Η παράσταση (α - β)(α2 + αβ + β2) γράφεται:

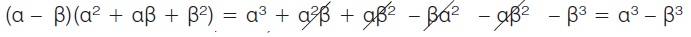
εικόνα

Αποδείξαμε λοιπόν την ταυτότητα

(α - β)(α2 + αβ + β2) = α3 - β3

Με τον ίδιο τρόπο μπορούμε να αποδείξουμε και την ταυτότητα

(α + β)(α2 - αβ + β2) = α3 + β3

Οι προηγούμενες ταυτότητες χρησιμοποιούνται για να βρίσκουμε γρήγορα γινόμενα παραστάσεων που έχουν τις αντίστοιχες μορφές. Για παράδειγμα έχουμε:

  • (x - 2)(x2 + 2x + 4) = (x - 2)(x2 + 2x + 22) = x3 - 23 = x3 - 8
  • (x + 3)(x2 - 3x + 9) = (x + 3)(x2 - 3x + 32) = x3 + 33 = x3 + 27
ΠΑΡΑΔΕΙΓΜΑΤΑ − ΕΦΑΡΜΟΓΕΣ
1

α) Να αποδειχθεί η ταυτότητα (α + β + γ)2 = α2 + β2 + γ2 + 2αβ + 2βγ + 2γα.

β) Να βρεθεί το ανάπτυγμα του (3x + 2y + 4)2.

 

Λύση

εικόνα

α) (α + β + γ)2 = (α + β + γ)(α + β + γ) =

α2 + αβ + αγ + βα + β2 + βγ + γα + γβ + γ2 =

α2 + β2 + γ2 + 2αβ + 2βγ + 2γα.

β) Σύμφωνα με την προηγούμενη ταυτότητα, το ανάπτυγμα του

(3x + 2y + 4)2 είναι: (3x + 2y + 4)2 =

(3x)2 + (2y)2 + 42 + 2·3x·2y + 2·2y·4 + 2·3x·4 =

9x2+ 4y2 + 16 + 12xy + 16y + 24x.

Μικροπείραμα μικροπείραμα    Μικροπείραμα μικροπείραμα

2

α) Να αποδειχθούν οι ταυτότητες α2 + β2 = (α + β)2 - 2αβ και α3 + β3 = (α + β)3 - 3αβ(α + β).

β) εικόνα

Λύση

α) Κάνουμε τις πράξεις στο δεύτερο μέλος κάθε ταυτότητας και έχουμε:

(α + β)2 - 2αβ = α2 + 2αβ + β2 - 2αβ = α2 + β2

(α + β)3 - 3αβ(α + β) = α3 + 3α2β + 3αβ2 + β3 - 3α2β - 3αβ2 = α3 + β3.

β)εικόνα

3

Σε ένα οικόπεδο που έχει σχήμα τετραγώνου πλευράς α, αν μειωθεί η μία διάστασή του κατά β και ταυτόχρονα η άλλη διάστασή του αυξηθεί κατά β, πόσο θα μεταβληθεί το εμβαδόν του;

Λύση

εικόνα

Το εμβαδόν του τετραγώνου είναι α2. Αν αλλάξουν οι πλευρές του, τότε το οικόπεδο θα γίνει ορθογώνιο με διαστάσεις α - β και α + β, οπότε θα έχει εμβαδόν (α - β)(α + β) = α2 - β2. Δηλαδή, το εμβαδόν από το α2 θα γίνει α2 - β2, που σημαίνει ότι θα μειωθεί κατά β2.

4

Να μετατραπεί το κλάσμα εικόναπου έχει άρρητο παρονομαστή σε ισοδύναμο κλάσμα με ρητό παρονομαστή.

Λύση

εικόνα

5

α) Να αποδειχθεί η ταυτότητα (ν - 1)(ν + 1) + 1 = ν2.

β) Να αποδειχθεί ότι ο αριθμός 2007·2009 + 1 είναι τετράγωνο ενός ακεραίου αριθμού, τον οποίο και να προσδιορίσετε.

 

Λύση

α) (ν - 1)(ν + 1) + 1 = (ν2 -12) + 1 = ν2 - 1 + 1 = ν2.

β) Αν ν = 2008, τότε ν - 1 = 2007 και ν + 1 = 2009.

Σύμφωνα με την προηγούμενη ταυτότητα έχουμε:

2007·2009 + 1 = (ν - 1)(ν + 1) + 1 = ν2 = 20082.

Άρα, ο αριθμός 2007·2009 + 1 είναι το τετράγωνο του ακεραίου 2008.

arrow Ορισμένοι αριθμητικοί υπολογισμοί γίνονται πιο σύντομα με τη βοήθεια των ταυτοτήτων π.χ.

99·101 = (100 - 1)(100 + 1) = 1002 - 12 = 10000 - 1 = 9999

1032 = (100 + 3)2 = 1002 + 2·100·3 + 32 = 10609

6

Να γίνουν οι πράξεις:

α) (2x - 3)2 - 2(3x - 1)(3x + 1)

β) (x - 2y)3 - (x - y)(x2 + xy + y2).

 

Λύση

α) (2x - 3)2 - 2(3x - 1)(3x + 1)

= [(2x)2 - 2·2x·3 + 32] - 2[(3x)2 - 12]

= (4x2 - 12x + 9) - 2(9x2 - 1)

= 4x2 - 12x + 9 - 18x2 + 2

= -14x2 - 12x + 11

β) (x - 2y)3 - (x - y)(x2 + xy + y2)

= [x3 - 3·x2·2y + 3·x·(2y)2 - (2y)3] - (x3 - y3)

= x3 - 6x2y + 12xy2 - 8y3 - x3 + y3

= -6x2y + 12xy2 - 7y3

7

Να αποδειχθεί ότι

(α2 + β2)(x2 + y2) = (αx + βy)2 + (αy - βx)2

(Ταυτότητα Lagrange).

Λύση

Το 1ο μέλος της ταυτότητας γράφεται:

(α2 + β2)(x2 + y2) = α2x2 + α2y2 + β2x2 + β2y2

Το 2ο μέλος της ταυτότητας γράφεται:

(αx + βy)2 + (αy - βx)2 = (αx)2 + 2(αx)(βy) + (βy)2 + (αy)2 - 2(αy)(βx) + (βx)2 =

α2x2 + 2αβxy + β2y2 + α2y2 - 2αβxy + β2x2 =

α2x2 + α2y2 + β2x2 + β2y2

Άρα (α2 + β2)(x2 + y2) = (αx + βy)2 + (αy - βx)2.

Όπως είδαμε στα προηγούμενα παραδείγματα για να αποδείξουμε μία ταυτότητα Α = Β,

μπορούμε να εργαστούμε ως εξής:

  • Ξεκινάμε από το ένα μέλος της ταυτότητας και καταλήγουμε στο άλλο (παραδείγματα 1, 2, 5) ή
  • − Κάνουμε τις πράξεις στο 1ο μέλος της ταυτότητας και καταλήγουμε σε μία ισότητα Α = Γ.
    − Κάνουμε τις πράξεις στο 2ο μέλος της ταυτότητας και καταλήγουμε σε μια ισότητα Β = Γ.

Αφού Α = Γ και Β = Γ συμπεραίνουμε ότι Α = Β (παράδειγμα 7).

ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ
1

Ποιες από τις παρακάτω ισότητες είναι ταυτότητες;

α) 0x = 0   β) x + y = 0     γ) α2α = α3    δ) (x + 3)2 = x2 + 6x + 9     ε) αβ = 0

2

Να επιλέξετε τη σωστή απάντηση.

  1. Το ανάπτυγμα του (x + α)2 είναι: εικόνα

    α) x2 + α2     β) x2 - 2xα + α2     γ) x2 + xα + α2     δ) x2 + 2xα + α2

  2. Το ανάπτυγμα του (2α + 1)2 είναι: εικόνα

    α) 2α2 + 4α + 1     β) 4α2 + 1     γ) 4α2 + 4α + 1     δ) 4α2 + 2α + 1

  3. Το ανάπτυγμα του (y - 2)2 είναι: εικόνα

    α) y2 - 2y + 4     β) y2 - 4     γ) y2 - 4y + 4     δ) y2 + 4y + 4

3

Να χαρακτηρίσετε τις παρακάτω ισότητες με (Σ), αν είναι σωστές ή με (Λ), αν είναι λανθασμένες.

  1. εικόνα (x - y)2 = x2 - 2x(-y) + (-y)2
  2. εικόνα (-α + β)2 = α2 - 2αβ + β2
  3. εικόνα (5ω + 4)2 = 25ω2 + 16
  4. εικόνα(3x - y)2 = 3x2 - 2·3x·y + y2
4

Να επιλέξετε τη σωστή απάντηση.

  1. Το ανάπτυγμα του (x + 1)3 είναι:
    1. x3 + 3·x·1 + 13
    2. x3 + 13
    3. x3 + 3·x2 ·1 + 3·x·12 + 13
    4. εικόνα x3 + x2·1 + x·12 + 13
  2. Το ανάπτυγμα του (β - 2)3 είναι:
    1. β3 - 3·β·2 + 23
    2. β3 - 23
    3. β3 - β2 ·2 + β·22 - 23
    4. εικόνα β3 - 3·β2 ·2 + 3·β·22 - 23
5

Να χαρακτηρίσετε τις παρακάτω ισότητες με (Σ), αν είναι σωστές ή με (Λ), αν είναι λανθασμένες.

  1. εικόνα (x - y)3 = x3 - 3x2y - 3xy2 - y3
  2. εικόνα (2x + 3)3 = 2x3 + 3·2x2·3 + 3·2x·32 + 33
  3. εικόνα (3x - 1)3 = (3x)3 - 3(3x)3·1 + 3(3x)·12 + 13
  4. εικόνα (x + 2)3 = x3 + 6x2 + 12x + 8
6

Να επιλέξετε τη σωστή απάντηση

  1. Το ανάπτυγμα του (y - 3)(y + 3) είναι: εικόνα

    α) y2 - 3       β) 9 - y2       γ) y2 - 9       δ) 3 - y2

  2. Το ανάπτυγμα του (y + x)(x - y) είναι: εικόνα

    α) y2 - x2       β) x2 - y2       γ) (x - y)2       δ) x2 + y2

  3. Το ανάπτυγμα του (ω - 2α)(ω + 2α) είναι:εικόνα

    α) ω2 - 2α2      β) ω2 + 4α2       γ) 4α2 - ω2       δ) ω2 - 4α2

  4. Το ανάπτυγμα του (5 - x)(52 + 5x + x2) είναι:εικόνα

    α) 53 + x3       β) x3 - 53      γ) 53 - x3       δ) 25 - x3

  5. Tο ανάπτυγμα του (x + 2α)(x2 − 2αx + 4α2) είναι:εικόνα

    α) x3 + 2α3       β) x3 - (2α)3      γ) x3 -2α3     δ) x3 + 8α3

7

Να συμπληρώσετε τον παρακάτω πίνακα αντιστοιχίζοντας σε κάθε παράσταση της στήλης Α, το ανάπτυγμά της από τη στήλη Β.

Στήλη Α Στήλη Β
    1. x2- 2xy + y2
α. (x + y)(y - x) 2. x3 - y3
β. (x + y)2 3. x3 - 3x2y + 3xy2 + y3
γ. (y - x)2 4. y2 - x2
δ. (x - y)(x2 + xy + y2) 5. x2 + 2xy + y2
ε. (x + y)(x2 - xy + y2) 6. x2 - y2
στ. (x - y)3 7. x3 + y3
    8. x3 - 3x2y  + 3xy2 -y3
α β γ δ ε στ
           
ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ − ΠΡΟΒΛΗΜΑΤΑ
1

1 Να βρείτε τα αναπτύγματα:

εικόνα

Μικροπείραμα μικροπείραμα    Μικροπείραμα μικροπείραμα

2

Να βρείτε τα αναπτύγματα:

εικόνα

3

Χρησιμοποιώντας την κατάλληλη ταυτότητα να υπολογίσετε τις παραστάσεις:

  1. (√3+1)2
  2. (√5+√6 )2
  3. (√2-3)2
  4. (1-√7)2

 

4

Να συμπληρώσετε τις ισότητες:

  1. (x … ……)2 = …… + …… + 9
  2. (…… … 4)2 = y2 - …… … ……
  3. (…… - ……)2 = 16x2 … 8xα … ……
  4. (…… … 2ω)2 = …… - 4x2ω … ……
5

Να βρείτε τα αναπτύγματα:

  1. (x + 1)3
  2. (y + 4)3
  3. (2α + 1)3
  4. (3α + 2β)3
  5. (x2 + 3)3
  6. (y2 + y)3
  7. (x - 2)3
  8. (y - 5)3
  9. (3α - 1)3
  10. (2x - 3y)3
  11. (y2 - 2)3
  12. (ω2 - 2ω)3
6

Να βρείτε τα αναπτύγματα:

  1. (x - 1)(x + 1)
  2. (y - 2)(y + 2)
  3. (3 - ω)(3 + ω)
  4. (x + 4)(4 - x)
  5. (x - y)(-x - y)
  6. (-x + y)(-x - y)
  7. (2x + 7y)(2x - 7y)
  8. (x-√2) (x+√2)
  9. (√x+√y) (√x-√y)
7

Να αποδείξετε ότι το πολυώνυμο P(x) = (x - 3)2 + (3x + 1)2- 10(x - 1)(x + 1) είναι σταθερό.

8

α) Να αποδείξετε ότι (α - β)(α + β)(α2 + β2)(α4 + β4) = α8 - β8.

β) Να υπολογίσετε το γινόμενο: 9·11·101·10001.

 

9

Να μετατρέψετε τα παρακάτω κλάσματα, που έχουν άρρητους παρονομαστές, σε ισοδύναμα κλάσματα με ρητούς παρονομαστές.
εικόνα

 

10

Να βρείτε τα αναπτύγματα:

  1. (x - 3)(x2 + 3x + 9)
  2. (y + 2)(y2 - 2y + 4)
  3. (2ω + 1)(4ω2 - 2ω + 1)
  4. (1 - α)(1 + α + α2)
11

Να κάνετε τις πράξεις:

  1. (x - 4)2 + (2x + 5)2
  2. (x2 - 1)2 - (x2 - 3)(x2 + 3)
  3. (x + y)2 - (x - 2y)(x + 2y) + (2x - y)2
  4. (3x - 4)2 + (3x + 4)2 - 2(3x - 4)(3x + 4)
  5. (2α + 1)3 + (2α - 1)2
  6. (α + 2)3 - (α + 2)(α2 - 2α + 4)
  7. (α2 + α)3 - (α2 - α)3
  8. (4α - 1)3 - α(8α + 1)(8α - 1)
12

Να αποδείξετε ότι:

  1. (x - 2y)2 - (2x - y)2 + 3x2 = 3y2
  2. (α - 3β)2+ (3α + 2β)(3α - 2β) - (3α - β)2 = α2 + 4β2
  3. (x - 1)(x + 1)3 - 2x(x - 1)(x + 1) = x4 - 1
  4. (α2 + β2)2 - (2αβ)2 = (α2 - β2)2
  5. (α - 4)2 + (2α - 3)2 = α2 + (2α - 5)2
  6. (2x2 + 2x)2 + (2x + 1)2 = (2x2 + 2x + 1)2
13

Αν x = 3 + √5 και y = 3 -√5 , να υπολογίσετε τις παραστάσεις:

α) xy        β) x2 - y2      γ) x2 + y2      δ) x3 + y3

 

14

εικόνα

15
εικόνα

Αν το τρίγωνο ΑΒΓ είναι ορθογώνιο, να αποδείξετε ότι και το τρίγωνο ΒΓΔ είναι ορθογώνιο.

 

16
  1. Σκεφτείτε δύο αριθμούς διαφορετικούς από το μηδέν.
  2. Βρείτε το τετράγωνο του αθροίσματός τους.
  3. Βρείτε το τετράγωνο της διαφοράς τους.
  4. Αφαιρέστε από το τετράγωνο του αθροίσματος το τετράγωνο της διαφοράς.
  5. Διαιρέστε το τελικό αποτέλεσμα με το γινόμενο των δύο αριθμών που αρχικά σκεφτήκατε.
  6. Το αποτέλεσμα που βρήκατε είναι ο αριθμός 4 ανεξάρτητα από τους αριθμούς που επιλέξατε. Μπορείτε να το εξηγήσετε;
17

α) Να αποδείξετε ότι  εικόνα

β) Να υπολογίσετε το εμβαδόν ορθογωνίου τριγώνου, που έχει υποτείνουσα 10 cm, και οι κάθετες πλευρές του διαφέρουν κατά 2 cm.

18

Ένας πατέρας μοίρασε ένα οικόπεδο στα δύο παιδιά του, όπως φαίνεται στο σχήμα. Τα δύο οικόπεδα είχαν το ίδιο εμβαδόν ή κάποιο από τα παιδιά αδικήθηκε; Να αιτιολογήσετε την απάντησή σας.

εικόνα

εικόνα

Παρατηρήστε τα αναπτύγματα των δυνάμεων του αθροίσματος α + β.

εικόνα

1. Οι αντίστοιχοι συντελεστές σε κάθε ανάπτυγμα σχηματίζουν μια γραμμή σ' ένα αριθμητικό τρίγωνο, που είναι γνωστό ως τρίγωνο του Πασκάλ. Το τρίγωνο αυτό πήρε το όνομά του από τον Γάλλο μαθηματικό Blaise Pascal (1623 - 1662) και οι αριθμοί του κρύβουν πολλές ιδιότητες. Ο πρώτος και ο τελευταίος αριθμός κάθε σειράς είναι 1. Μπορείτε να ανακαλύψετε με ποιον τρόπο προκύπτουν οι υπόλοιποι αριθμοί κάθε σειράς;

2. Συνεχίστε την κατασκευή του τριγώνου και βρείτε τα αναπτύγματα (α + β)5 και (α + β)6, αφού πρώτα ανακαλύψετε με ποιον τρόπο γράφονται οι δυνάμεις του α και του β σε κάθε ανάπτυγμα.

3. Να βρείτε και το ανάπτυγμα του (α - β)6, αν γνωρίζετε ότι και τα αναπτύγματα των δυνάμεων της διαφοράς α - β προκύπτουν με τον ίδιο ακριβώς τρόπο, μόνο που θέτουμε τα πρόσημα εναλλάξ, αρχίζοντας από +. π.χ. (α - β)2 = α2 - 2αβ + β2, (α - β)3 = α3 - 3α2β + 3αβ2 - β3

4. Μπορείτε να βρείτε ποιες άλλες ιδιότητες κρύβουν οι αριθμοί του τριγώνου Πασκάλ;

Μικροπείραμα μικροπείραμα    Μπλεζ Πασκάλ

 

εικόνα

Πυθαγόρειες τριάδες

εικόνα

Αν οι αριθμοί α, β, γ εκφράζουν τα μήκη των πλευρών ενός ορθογωνίου τριγώνου, τότε όπως γνωρίζουμε, ισχύει το Πυθαγόρειο θεώρημα

α2 = β2 + γ2 (1)

Πόσα όμως ορθογώνια τρίγωνα μπορούμε να βρούμε που τα μήκη των πλευρών τους εκφράζονται με ακέραιους αριθμούς; Μια τριάδα θετικών ακεραίων αριθμών α, β, γ, για την οποία ισχύει η σχέση (1), λέμε ότι αποτελεί Πυθαγόρεια τριάδα. Την απλούστερη Πυθαγόρεια τριάδα σχηματίζουν οι αριθμοί 5, 4, 3 αφού 52 = 42 + 32. Υπάρχουν, άραγε, τρόποι να σχηματίζουμε Πυθαγόρειες τριάδες; Ο Πυθαγόρας (6ος αιώνας π.Χ.) γνώριζε ότι οι αριθμοί της μορφής

εικόνα

σχηματίζουν μια Πυθαγόρεια τριάδα.

  1. Μπορείτε να το αποδείξετε;
  2. Να βρείτε δύο τουλάχιστον Πυθαγόρειες τριάδες με τους αριθμούς του Πυθαγόρα.
εικόνα

Ο Πλάτωνας (5ος - 4ος αιώνας π.Χ.) γνώριζε ότι οι

εικόνα

σχηματίζουν μια Πυθαγόρεια τριάδα.

  1. Μπορείτε να το αποδείξετε;
  2. Να βρείτε δύο τουλάχιστον Πυθαγόρειες τριάδες με τους αριθμούς του Πλάτωνα.
εικόνα

O Διόφαντος (3ος αιώνας μ.Χ.) στηριζόμενος σε μία ταυτότητα την οποία γνώριζε και ο Ευκλείδης, έδωσε μια γενικότερη λύση στο πρόβλημα κατασκευής Πυθαγορείων τριάδων από οποιουσδήποτε αριθμούς (άρτιους ή περιττούς). Ανακάλυψε ότι ο αριθμοί της μορφής λ2 + μ2, λ2 - μ2, 2λμ, όπου λ, μ θετικοί άνισοι ακέραιοι αριθμοί, σχηματίζουν Πυθαγόρεια τριάδα.

  1. Μπορείτε να το αποδείξετε;
  2. Να βρείτε δύο τουλάχιστον Πυθαγόρειες τριάδες με τους αριθμούς του Διόφαντου.

Μικροπείραμα μικροπείραμα    Μικροπείραμα μικροπείραμα

 

εικόνα