5.1 Έργο και Ενέργεια

μια μικρή ιστορία ...

Βόγιατζερ, οι μικροί ταξιδιώτες του διαστήματος

Το 1977 εκτοξεύθηκαν από τις Η.Π.Α. δύο διαστημόπλοια με το όνομα Βόγιατζερ (Voyager) με σκοπό να συγκεντρώσουν πληροφορίες για τους εξωτερικούς πλανήτες του ηλιακού μας συστήματος. Σήμερα και τα δυο Βόγιατζερ συνεχίζουν το ταξίδι τους έξω από το ηλιακό μας σύστημα και μας στέλνουν πληροφορίες για τον κόσμο έξω από αυτό. Στα διαστημόπλοια υπάρχει ηχογραφημένο μήνυμα σε 55 διαφορετικές γλώσσες μεταξύ των οποίων και τα αρχαία Ελληνικά, καθώς και διάφοροι ήχοι από τη γη προκειμένου να αξιοποιηθούν για την αναγνώρισή μας από τυχόν εξωγήινα, νοήμονα όντα. Η πραγματοποίηση ενός τέτοιου ταξιδιού απαιτούσε τεράστια ποσά ενέργειας. Κάθε διαστημόπλοιο, που ζύγιζε 815 kg, χρειάστηκε στην εκτόξευσή του 700.000 kg καύσιμα. Η χημική ενέργεια αυτών των καυσίμων μετατράπηκε σε θερμική. Η ενέργεια για τη λειτουργία των οργάνων προήλθε από τη διαδοχική μετατροπή πυρηνικής σε θερμική και τελικά σε ηλεκτρική ενέργεια. Συμπληρωματικά χρησιμοποιήθηκε και η ενέργεια ακτινοβολίας από τον ήλιο.

Σε αυτό το κεφάλαιο θα μάθουμε για τις διάφορες μορφές ενέργειας, τη μετατροπή της ενέργειας από μια μορφή σε άλλη καθώς και για τη διατήρηση της ενέργειας.

ΚΕΦΑΛΑΙΟ 5

ΕΝΕΡΓΕΙΑ

Εικόνα 5.1.

«Πυρ το αείζωον» Φωτιά η αιώνια: Αιτία διαρκούς αλλαγής. ΗΡΑΚΛΕΙΤΟΣ

Εικόνα 5.2. Κουβέιτ.

Πετρελαϊκός σταθμός που καίγεται κατά τη διάρκεια του πολέμου του Περσικού Κόλπου. Η χρησιμοποίηση ενέργειας είναι απαραίτητη για τη λειτουργία της ανθρώπινης κοινωνίας. Όμως σε πολλές περιπτώσεις, μπορεί να προκαλέσει οικολογικές καταστροφές.

Εικόνα 5.3.

Διαφορετικά στιγμιότυπα από την κίνηση ενός βλήματος καθώς διαπερνά ένα μήλο. Αρχικά κινείται με ταχύτητα 800 m/s. Έχει ενέργεια. Προκαλεί μεταβολές.

ΕΝΕΡΓΕΙΑ: ΜΙΑ ΘΕΜΕΛΙΩΔΗΣ ΕΝΝΟΙΑ ΤΗΣ ΦΥΣΙΚΗΣ

Οι αρχαίοι Έλληνες φιλόσοφοι αναζήτησαν τα στοιχεία από τα οποία αποτελείται ο κόσμος και προσπάθησαν να ερμηνεύσουν τις μεταβολές που συμβαίνουν στη φύση. Ο Αριστοτέλης πίστευε ότι ο κόσμος συγκροτείται από τέσσερα στοιχεία, τη φωτιά, το νερό, τη γη και τον αέρα. Από αυτά το «πυρ», δηλαδή η φωτιά, συμβόλιζε τις συνεχείς αλλαγές που βλέπουμε γύρω μας. Ο Ηράκλειτος θεωρούσε ότι μόνο το πυρ είναι το πρωταρχικό στοιχείο από το οποίο γεννιούνται όλα τα όντα και σε αυτό επανέρχονται. Το πυρ δε χάνεται, αλλά παίρνει κάθε τόσο διαφορετικές μορφές και περνάει από διάφορες καταστάσεις. Όλα τα υπόλοιπα αλλάζουν: «τα πάντα ρει». Έτσι, για πρώτη φορά στην ιστορία εμφανίζεται η αντίληψη της διατήρησης ενός μεγέθους (πυρ) το οποίο μπορεί να αλλάζει μορφές, αλλά τελικά διατηρείται (εικόνα 5.1).

Η παραπάνω άποψη του Ηράκλειτου επανήλθε στο προσκήνιο τον 17ο αιώνα με την εισαγωγή μιας καινούργιας για την εποχή αυτή έννοιας: της ενέργειας. Ο όρος χρησιμοποιήθηκε αρχικά από τον Γαλιλαίο, χωρίς όμως επιστημονικό ορισμό. Η ρίζα της λέξης είναι αρχαιοελληνική από το εν (μέσα) και έργο, δηλαδή σημαίνει την εσωτερική ικανότητα κάποιου να παράγει έργο. Μόλις όμως πριν από 200 περίπου χρόνια η έννοια απέκτησε επιστημονικό περιεχόμενο. Οι φυσικοί αξιοποιώντας την έννοια της ενέργειας κατάφεραν να περιγράψουν με ενιαίο τρόπο φαινόμενα, όπως τα κινητικά, τα θερμικά, τα ηλεκτρικά, τα φωτεινά, τα ηχητικά και τα χημικά, τα οποία ως τότε αντιμετωπίζονταν ως ανεξάρτητα μεταξύ τους.

Στις αρχές του εικοστού αιώνα, η έννοια της ενέργειας αποτέλεσε τη βάση για να διατυπωθούν δύο από τις σύγχρονες φυσικές θεωρίες: η θεωρία της σχετικότητας και η κβαντική θεωρία και εξελίχθηκε σε κεντρική ενοποιητική έννοια της γλώσσας που χρησιμοποιούν οι φυσικοί για να περιγράψουν τα φαινόμενα που μελετά η επιστήμη της φυσικής. Επιπλέον, η ενέργεια είναι η έννοια που συνδέει τη φυσική με τις άλλες φυσικές επιστήμες και την Τεχνολογία.

Σήμερα όλοι είμαστε εξοικειωμένοι με την έννοια της ενέργειας (εικόνα 5.2). Ενέργεια με τη μορφή της ακτινοβολίας έρχεται στη γη από τον ήλιο, περιέχεται στις τροφές που τρώμε και διατηρεί τη ζωή. Παρόλο που η ενέργεια είναι η πιο διαδεδομένη έννοια στις φυσικές επιστήμες, ο ορισμός της είναι ιδιαίτερα δύσκολος. Πώς θα προσεγγίσουμε την έννοια της ενέργειας;

Ο δρομέας όταν τρέχει, έχει ενέργεια. Ο άλτης όταν πηδά, έχει επίσης ενέργεια. Μια γλάστρα που πέφτει από ένα μπαλκόνι έχει

ΚΕΦΑΛΑΙΟ 5 ΕΝΕΡΓΕΙΑ

αρκετή ενέργεια και βουλιάζει την οροφή ενός αυτοκινήτου. Οι άνθρωποι, τα ζώα, τα φυτά, τα διάφορα αντικείμενα έχουν ενέργεια. Ωστόσο, παρατηρούμε τα αποτελέσματα της ενέργειας μόνο όταν εκδηλώνεται ένα φαινόμενο, μια μεταβολή. Λέμε ότι όταν η ενέργεια μεταφέρεται από ένα σώμα σε άλλο ή μετατρέπεται από μια μορφή σε άλλη, προκαλεί μεταβολές (εικόνα 5.3).

Γενικότερα, η ενέργεια εμφανίζεται με διάφορες μορφές, μετατρέπεται από μια μορφή σε άλλη, αλλά κατά τις μετατροπές της η συνολική ενέργεια διατηρείται. Ο υπολογισμός της ενέργειας που μετατρέπεται από μια μορφή σε άλλη ή μεταφέρεται από ένα σώμα σε άλλο διευκολύνεται σε μερικές περιπτώσεις με την εισαγωγή ενός νέου φυσικού μεγέθους: του έργου.

5.1 Έργο και Ενέργεια

Η λέξη έργο χρησιμοποιείται στην καθημερινή ζωή με διαφορετική σημασία από αυτήν με την οποία τη χρησιμοποιούμε στη φυσική. Για παράδειγμα, οι περισσότεροι λένε ότι η κατασκευή της γέφυρας "Ρίου-Αντιρίου" ήταν ένα δύσκολο έργο.

Η πρώτη αντίληψη για την έννοια του έργου φαίνεται ότι προέρχεται από τους αρχαίους Έλληνες. Δημιουργήθηκε ως αποτέλεσμα της προσπάθειάς τους να ερμηνεύσουν πώς είναι δυνατόν να ανυψωθεί ένα βαρύ αντικείμενο ασκώντας μικρή δύναμη με τη βοήθεια ενός μοχλού (εικόνα 5.4). Στις αρχές του 17ου αιώνα ο Γαλιλαίος συνέλαβε τον ουσιαστικό χαρακτήρα της έννοιας. Παρατηρώντας τον τρόπο που τοποθετούσαν πασσάλους στο έδαφος, διαπίστωσε ότι το αποτέλεσμα ήταν συνδυασμός του βάρους του σφυριού που χρησιμοποιούσαν και του ύψους από το οποίο έπεφτε (εικόνα 5.5). Η δύναμη (βάρος) και η μετατόπιση (ύψος) φαίνεται να συνδέονται με κάποιο τρόπο. Το 1829 ο Γάλλος φυσικός Κοριόλις αποκάλεσε το γινόμενο της δύναμης με τη μετατόπιση, έργο.

Σήμερα, με την έννοια του έργου περιγράφουμε τη μεταφορά ή τη μετατροπή της ενέργειας κατά τη δράση μιας δύναμης. Για παράδειγμα, όταν τακτοποιείς τη βιβλιοθήκη σου και ανεβάζεις τα βιβλία από το χαμηλότερο ράφι της στο υψηλότερο, θα κουραστείς. Τα βιβλία, μέσω της δύναμης που τους ασκείς, αποκτούν ενέργεια. Από τον οργανισμό σου μεταφέρεται ενέργεια στα βιβλία και για να την αναπληρώσεις, θα χρειαστεί να φας. Χρησιμοποιούμε το φυσικό μέγεθος έργο για να εκφράσουμε την ποσότητα ενέργειας που μεταφέρεται από εσένα στα βιβλία.

Έργο δύναμης

Όταν ανυψώνεται οποιοδήποτε σώμα, ασκείται σ' αυτό μια δύναμη τουλάχιστον ίση με το βάρος του. Λέμε ότι η δύναμη παράγει έργο πάνω στο σώμα. Στην εικόνα 5.6 ο αθλητής ανυψώνει την μπάρα ασκώντας σ' αυτή δύναμη. Όσο η μπάρα ανεβαίνει, η δύναμη παράγει έργο πάνω της. Όταν ο αθλητής κρατάει ακίνητη την μπάρα, η δύναμη δεν παράγει έργο.

Εικόνα 5.4.

Το κοριτσάκι της εικόνας ανυψώνει εύκολα τον πατέρα του. Όσο πιο κοντά βρίσκεται ο πατέρας στον άξονα περιστροφής, τόσο μικρότερη είναι δύναμη που ασκεί το κοριτσάκι. Η ιδέα να συνδεθεί η δύναμη που ασκείται σε ένα σώμα με τη μετατόπιση αποδίδεται στον Αρχιμήδη (3ος π.Χ. αιώνας) και στον Ήρωνα τον Αλεξανδρέα (1ος μ.Χ. αιώνας).

Εικόνα 5.5.

Όσο ψηλότερα σηκώνει το χέρι του ο εργάτης και όσο βαρύτερο είναι το σφυρί, τόσο βαθύτερα το καρφί εισχωρεί στο πάτωμα. Αυτή η παρατήρηση οδήγησε τον Γαλιλαίο να συνδέσει τη δύναμη με τη μετατόπιση.

Εικόνα 5.6.

Ο αθλητής ασκεί δύναμη (F) στην μπάρα που προκαλεί την ανύψωσή της σε ύψος h. Λέμε ότι η F παράγει έργο στην μπάρα. Ενέργεια μεταφέρεται από τον αθλητή στην μπάρα. Ο αθλητής κουράζεται.

ΦΥΣΙΚΗ Β' ΓΥΜΝΑΣΙΟΥ

Εικόνα 5.7.

Το έργο μιας δύναμης μπορεί να είναι θετικό ή αρνητικό. (α) Το άλογο ασκεί δύναμη στο κάρο. Το κάρο μετατοπίζεται. Η δύναμη και η μετατόπιση έχουν την ίδια κατεύθυνση. Η δύναμη παράγει θετικό έργο. (β) Η τσουλήθρα ασκεί δύναμη στο παιδί, την τριβή, που αντιστέκεται στην κίνησή του. Η τριβή και η μετατόπιση είναι αντίθετες. Το έργο της τριβής είναι αρνητικό.

Εικόνα 5.8.

Το αγόρι που κάθεται στο μεταξωτό χαλάκι μετατοπίζεται πάνω στο πάτωμα κατά Δx από μια οριζόντια δύναμη F που ασκείται από το κορίτσι. Η δύναμη του βάρους w και η F_N είναι κατακόρυφες και επομένως κάθετες στη μετατόπιση. Δεν παράγουν έργο ή το έργο τους είναι ίσο με το 0. Η δύναμη F που ασκεί το κορίτσι είναι παράλληλη στη μετατόπιση και παράγει έργο.

Από τι εξαρτάται το έργο μιας δύναμης;

Όσο βαρύτερο είναι ένα σώμα το οποίο ανυψώνεις, τόσο περισσότερο κουράζεσαι, διότι παράγεις μεγαλύτερο έργο. Δηλαδή, το έργο εξαρτάται από τη δύναμη που ασκείται στο σώμα. Επιπλέον, η δραστηριότητα γίνεται πιο κουραστική, αν το σώμα πρέπει να ανυψωθεί σε μεγαλύτερο ύψος. Άρα, το έργο εξαρτάται και από τη μετατόπιση του σώματος.

Γενικά, μια δύναμη που ασκείται σ' ένα σώμα μπορεί να παράγει έργο (W) πάνω σ' αυτό όταν το σώμα μετακινείται. Στην απλούστερη περίπτωση, όπου η δύναμη είναι σταθερή και το σώμα μετακινείται κατά τη διεύθυνσή της, το έργο ορίζεται ως το γινόμενο της δύναμης επί τη μετατόπιση του σώματος.

Δηλαδή:

Έργο = Δύναμη x Μετατόπιση

ή συμβολικά:

W=F · Δx (5.1)

Μονάδες έργου

Το έργο είναι παράγωγο μέγεθος και επομένως η μονάδα του προκύπτει από τον ορισμό του. Από τη σχέση 5.1 βλέπουμε ότι η μονάδα του έργου είναι η μονάδα της δύναμης επί τη μονάδα του μήκους. Στο διεθνές σύστημα μονάδων (S.I.), η δύναμη μετριέται σε Ν (Newton) και η μετατόπιση σε μέτρα (m), οπότε το έργο μετριέται σε N.m. Η μονάδα αυτή ονομάζεται Joule (Τζάουλ) ή συντετμημένα J προς τιμή του Άγγλου φυσικού Τζέιμς Πρέσκοτ Τζάουλ (J=Joule).

Είναι λοιπόν:

1 J=1 N · m

και τα πολλαπλάσιά του, 1 kJ = 10³ J και 1 MJ = 10⁶ J.

Άρα: Έργο 1 Joule παράγει δύναμη 1 Ν που ασκείται σε σώμα το οποίο μετατοπίζεται κατά 1 m, κατά την κατεύθυνση της δύναμης.

Για ένα μήλο που πέφτει από ύψος 1 m, το έργο του βάρους του είναι μερικά J, ο αρσιβαρίστας παράγει έργο μερικά kJ, ενώ το έργο για το σταμάτημα ενός φορτωμένου φορτηγού που κινείται με 100 km/h είναι μερικά MJ.

Περιπτώσεις έργου

Το έργο μπορεί να είναι θετικό, αρνητικό ή μηδέν. Είναι θετικό όταν η δύναμη έχει την ίδια κατεύθυνση με τη μετατόπιση του σώματος. Δηλαδή, όταν η δύναμη προκαλεί την κίνηση, όπως συμβαίνει με τη δύναμη που ασκεί το άλογο στην εικόνα 5.7.α.

Είναι αρνητικό όταν η δύναμη έχει αντίθετη κατεύθυνση από τη μετατόπιση του σώματος. Δηλαδή, όταν η δύναμη αντιτίθεται στην κίνηση, όπως συμβαίνει με τη δύναμη της τριβής στην εικόνα 5.7.β.

Είναι μηδέν όταν η διεύθυνση της δύναμης είναι κάθετη στη διεύθυνση της μετατόπισης. Για παράδειγμα, για μια οριζόντια

ΚΕΦΑΛΑΙΟ 5 ΕΝΕΡΓΕΙΑ

κίνηση το έργο του βάρους w ή της δύναμης στήριξης F_N ισούται με το μηδέν (εικόνα 5.8). Η δύναμη F παράγει έργο, ενώ οι F_N και w, όχι.

Υπολογισμός έργου σταθερής δύναμης

A. Δύναμη παράλληλη με τη μετατόπιση

Ένα μήλο πέφτει στο έδαφος από ύψος h. Πόσο έργο παράγει το βάρος πάνω στο μήλο;

Επειδή το μήλο κινείται σε κατακόρυφη διεύθυνση, δύναμη και μετατόπιση έχουν την ίδια κατεύθυνση, οπότε προκύπτει:

W_w = w · Δ_x, W_w = w · h

Όταν ένας αρσιβαρίστας ανυψώνει μια μπάρα βάρους w σε ύψος h, ασκεί συνολική δύναμη (F) σε αυτή αντίθετη με το βάρος της (F=w).

Πόσο είναι το έργο του βάρους της μπάρας κατά την ανύψωσή της και πόσο το έργο της δύναμης F που ασκεί ο αθλητής στην μπάρα;

Το βάρος (w) της μπάρας και η μετατόπισή της έχουν αντίθετες κατευθύνσεις (εικόνα 5.9). Επομένως, το έργο του βάρους της μπάρας είναι αρνητικό:

W_w = - w · h

Αντίθετα, η δύναμη F που ασκεί ο αρσιβαρίστας στην μπάρα και η μετατόπισή της έχουν την ίδια κατεύθυνση (εικόνα 5.9). Επομένως, το έργο της F είναι θετικό:

W_F= F · H

B. Δύναμη πλάγια σε σχέση με τη μετατόπιση

Σύρουμε μια βαλίτσα πάνω σε οριζόντιο έδαφος (εικόνα 5.10). Πόσο έργο παράγει η δύναμη που ασκούμε στη βαλίτσα;

Αναλύουμε τη δύναμη σε δύο συνιστώσες (F₁ και F₂): H F₁ είναι παράλληλη και η F₂ κάθετη προς τη μετατόπιση. Το έργο της συνιστώσας που είναι κάθετη στη μετατόπιση είναι πάντοτε ίσο με μηδέν: Επομένως, το έργο της δύναμης (F) ισούται με το γινόμενο της παράλληλης συνιστώσας (F₁) επί τη μετατόπιση:

W_F = W_F1 = F₁ · Δ_x

Πόσο έργο παράγεται από το βάρος του παιδιού, όταν αυτό κατεβαίνει την τσουλήθρα (εικόνα 5.7);

Η τσουλήθρα είναι ένα επίπεδο πλάγιο ως προς το οριζόντιο έδαφος. Κάθε τέτοιο επίπεδο ονομάζεται κεκλιμένο ή πλάγιο επίπεδο.

Το βάρος του παιδιού που κινείται στο κεκλιμένο επίπεδο έχει κατεύθυνση πλάγια σε σχέση με τη μετατόπιση του παιδιού (εικόνα 5.11). Έτσι, για να υπολογίσουμε το έργο του βάρους του, πρέπει να το αναλύσουμε σε δύο συνιστώσες: μια κάθετη στο κεκλιμένο επίπεδο (w₁) και μια παράλληλη σε αυτό (w₂). Οπότε,

Εικόνα 5.9.

Ανεβάζουμε πολύ αργά με το χέρι μας το τούβλο κατά ύψος h. Η δύναμη F είναι ελάχιστα μεγαλύτερη από το βάρος και έχει την ίδια κατεύθυνση με τη μετατόπιση. Το έργο της είναι θετικό: W=F·Δx=F·h. Η φορά του βάρους και της μετατόπισης είναι αντίθετες. To έργο του βάρους είναι αρνητικό: W_F=-w·Δx= -w·h.

Εικόνα 5.10.

Η δύναμη F αναλύεται στην F₁ και την F₂. Η F₂ δεν παράγει έργο, γιατί είναι κάθετη στη μετατόπιση. H F₁ είναι παράλληλη στη μετατόπιση και παράγει έργο.

Εικόνα 5.11.

Το βάρος αναλύεται σε δύο συνιστώσες, την w₁ και w₂. Η w₁ είναι κάθετη στη μετατόπιση και δεν παράγει έργο. Η w₂ είναι παράλληλη και παράγει έργο.

ΦΥΣΙΚΗ Β' ΓΥΜΝΑΣΙΟΥ

σύμφωνα με τα προηγούμενα, το έργο (W_w) του βάρους του παιδιού προκύπτει:

W_w = W_w₂= w₂ · Δx

Δραστηριότητα

Έργο δύναμης

Να συνδέσεις με τη βοήθεια ενός νήματος ένα δυναμόμετρο με κιβώτιο μάζας 1 kg.
Τράβηξε το κιβώτιο ώστε να κινείται με σταθερή ταχύτητα πάνω στο θρανίο σου, κρατώντας το νήμα παράλληλο προς το θρανίο.
Ποια είναι η ένδειξη του δυναμομέτρου;
Γιατί πρέπει να ασκείς δύναμη στο κιβώτιο ώστε να κινείται με σταθερή ταχύτητα;
Υπολόγισε το έργο αυτής της δύναμης, όταν μετατοπίζεις το κιβώτιο από τη μία άκρη του θρανίου σου στην άλλη.

Παράδειγμα 5.1

Ένας αθλητής της άρσης βαρών ανυψώνει την μπάρα που έχει βάρος 2.000 Ν από το έδαφος σε ύψος 2 m. Πόσο έργο παρήγαγε ο αθλητής;

Δεδομένα	Ζητούμενα	Βασική εξίσωση
W = 2.000 Ν	W_w (έργο)	W=F·Δx
Δx = 2 m

Λύση

Βήμα 1: Σχεδιάζουμε τις δυνάμεις που ασκούνται στη μπάρα:

α) Από απόσταση το βάρος w, β) από επαφή η δύναμη F που ασκεί ο αθλητής.

Βήμα 2: Υπολογίζουμε τη δύναμη που ασκεί ο αθλητής στην μπάρα. Για να ανυψώσει την μπάρα, ο αθλητής θα πρέπει να ασκήσει δύναμη F τουλάχιστον ίση με το βάρος τους.

Βήμα 3: Εφαρμόζουμε τη βασική εξίσωση:

Η δύναμη F και η μετατόπιση Δx έχουν ίδιες κατευθύνσεις. Άρα

W = F·Δx, ή W = 2.000 N·2 m, ή W = 4.000 J

Φυσική και Μαθηματικά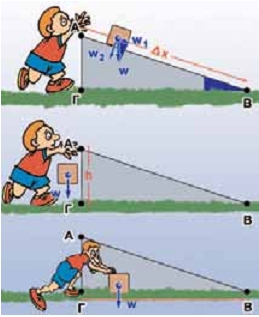

Το έργο του βάρους δεν εξαρτάται από τη μετατόπιση παρά μόνο από τη διαφορά ύψους μεταξύ αρχικής και τελικής θέσης.

Άφησε ένα σώμα να πέσει κατά μήκος ενός κεκλιμένου επιπέδου (ΑΒ). Υπολόγισε το έργο του βάρους.

Άφησε το σώμα να πέσει κατακόρυφα από το Α στο Γ και στη συνέχεια σπρώξε το πάνω στο οριζόντιο επίπεδο από το Γ έως το Β. Υπολόγισε τώρα το έργο του βάρους.

Απόδειξε ότι: w₁/ΑΓ = w/ΑΒ ή w₁·Δx = w·h, ή W_w₁ = W_W δηλαδή ότι το έργο του βάρους είναι το ίδιο είτε το σώμα ακολουθεί το δρόμο ΑΒ είτε κινείται κατακόρυφα από το Α στο Γ, οπότε το έργο είναι W_W = w·h και στη συνέχεια κινείται οριζόντια μέχρι το Γ, οπότε το έργο του βάρους είναι μηδέν.

Παρατήρησε τα δυο γραμμοσκιασμένα τρίγωνα του σχήματος. Παρατήρησε ότι έχουν ίσες γωνίες. Θυμήσου από τα μαθηματικά σου τον ορισμό του ημίτονου γωνίας.