B4.4: Η πυραμίδα και τα στοιχεία της

4.4.	Η πυραμίδα και τα στοιχεία της

Από την αρχαιότητα οι άνθρωποι έκτιζαν μνημεία με τη μορφή πυραμίδας.

Οι τάφοι των βασιλέων της αρχαίας Αιγύπτου είχαν τη γνωστή σ' εμάς μορφή της πυραμίδας.

Οι Αζτέκοι και οι Ίνκας είχαν χτίσει, επίσης, ναούς στο σχήμα πυραμίδας, αρκετοί από τους οποίους σώζονται μέχρι σήμερα.

Στην είσοδο του μουσείου του Λούβρου, στο Παρίσι, υπάρχει μια σύγχρονη πυραμίδα που σχεδιάστηκε το 1989 από τον αρχιτέκτονα Γιέο Μιγκ Πέι.

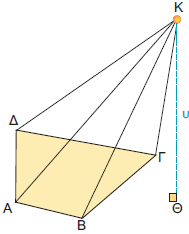
Πυραμίδα λέγεται ένα στερεό, που μία έδρα του είναι ένα πολύγωνο και όλες οι άλλες έδρες του είναι τρίγωνα με κοινή κορυφή.

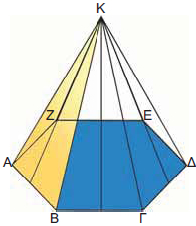
Για παράδειγμα, μια πυραμίδα με μια έδρα το επτάγωνο ΑΒΓΔΕΖΗ φαίνεται στο παρακάτω σχήμα:

Τα στοιχεία της πυραμίδας

	Το πολύγωνο ΑΒΓΔΕΖΗ λέγεται βάση της πυραμίδας.
	Τα τρίγωνα με κοινή κορυφή το σημείο Κ: ΚΑΒ, ΚΒΓ, ΚΓΔ, ΚΔΕ, ΚΕΖ, ΚΖΗ και ΚΗΑ λέγονται παράπλευρες έδρες της πυραμίδας.
	Το κοινό σημείο Κ των παράπλευρων εδρών λέγεται κορυφή της πυραμίδας.
	Αν από την κορυφή Κ φέρουμε κάθετο ευθύγραμμο τμήμα ΚΘ προς τη βάση, τότε το ΚΘ λέγεται ύψος της πυραμίδας. Παρατηρούμε στο διπλανό σχήμα ότι το ύψος μιας πυραμίδας μπορεί να βρίσκεται και εκτός της πυραμίδας.
	Μια πυραμίδα που έχει ως βάση ένα τρίγωνο, λέγεται τριγωνική πυραμίδα. Επειδή όμως η τριγωνική πυραμίδα έχει τέσσερις τριγωνικές έδρες και οποιαδήποτε έδρα της μπορεί να θεωρηθεί ως βάση, τη λέμε και τετράεδρο. Μικροπείραμα Μικροπείραμα
	Mια πυραμίδα που έχει βάση τετράπλευρο λέγεται τετραπλευρική.
	Μια πυραμίδα που έχει βάση πεντάγωνο λέγεται πενταγωνική κ.ο.κ.

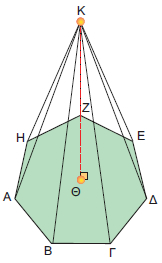
Κανονική πυραμίδα

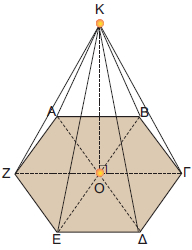
Μια πυραμίδα λέγεται κανονική, αν η βάση της είναι κανονικό πολύγωνο και η προβολή της κορυφής της στη βάση είναι το κέντρο του κανονικού πολυγώνου, όπως φαίνεται στο διπλανό σχήμα.

Σε οποιαδήποτε κανονική πυραμίδα οι παράπλευρες έδρες είναι ίσα μεταξύ τους ισοσκελή τρίγωνα (ΚΑΒ, ΚΒΓ, ΚΓΔ, ΚΔΕ, ΚΕΖ, ΚΖΑ).

Αντίστροφα, αν οι παράπλευρες έδρες μίας πυραμίδας είναι ίσα μεταξύ τους ισοσκελή τρίγωνα, τότε η πυραμίδα είναι κανονική.

Εμβαδόν επιφάνειας πυραμίδας

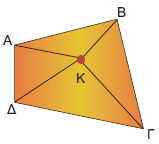
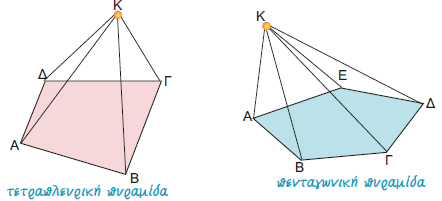
Η ολική επιφάνεια της πυραμίδας αποτελείται από δύο μέρη: την επιφάνεια των παράπλευρων εδρών της, που ονομάζεται παράπλευρη επιφάνεια και την επιφάνεια της βάσης της.

Για να υπολογίσουμε το εμβαδόν της παράπλευρης επιφάνειας Ε_Π μιας πυραμίδας, υπολογίζουμε το εμβαδόν κάθε παράπλευρης έδρας (που είναι τρίγωνο) και προσθέτουμε τα εμβαδά αυτά.

Επομένως, στο διπλανό σχήμα έχουμε:

Ε_Π = (Κ₁ΑΒ) + (Κ₂ΒΓ) + (Κ₃ΓΔ) + (Κ₄ΔΑ).

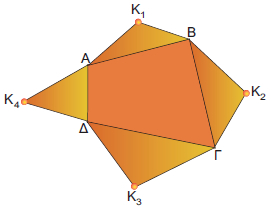Για να υπολογίσουμε το εμβαδόν της ολικής επιφάνειας Ε_ολ της πυραμίδας, προσθέτουμε στο εμβαδόν της παράπλευρης επιφάνειας το εμβαδόν της βάσης Ε_β.

Στο προηγούμενο σχήμα έχουμε ότι:

Ε_ολ = Ε_π + Ε_β = (Κ₁ΑΒ) + (Κ₂ΒΓ) + (Κ₃ΓΔ) + (Κ₄ΔΑ) + (ΑΒΓΔ).

Εμβαδόν επιφάνειας κανονικής πυραμίδας

Όταν η πυραμίδα είναι κανονική, τότε η παράπλευρη επιφάνειά της αποτελείται από ίσα μεταξύ τους ισοσκελή τρίγωνα, τα οποία έχουν όλα ίσες βάσεις και ίσα ύψη. Καθένα από αυτά τα ύψη λέγεται απόστημα της κανονικής πυραμίδας.

Ας υπολογίσουμε το εμβαδόν της παράπλευρης επιφάνειας μιας κανονικής εξαγωνικής πυραμίδας:

Ε_Π=(ΚΑΒ) + (ΚΒΓ) + (ΚΓΔ) + (ΚΔΕ) + (ΚΕΖ) + (ΚΖΑ) = 6(ΚΑΒ)

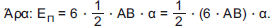
Όμως, η περίμετρος του κανονικού εξαγώνου ισούται με 6 • ΑΒ.

Τελικά, καταλήγουμε ότι:

Το συμπέρασμα αυτό ισχύει τελικά για κάθε κανονική πυραμίδα:

Για να βρούμε το εμβαδόν της ολικής επιφάνειας της κανονικής πυραμίδας, αρκεί να προσθέσουμε στο εμβαδόν της παράπλευρης επιφάνειας Ε_Π και το εμβαδόν του κανονικού πολυγώνου, που αποτελεί τη βάση της κανονικής πυραμίδας.

Μικροπείραμα

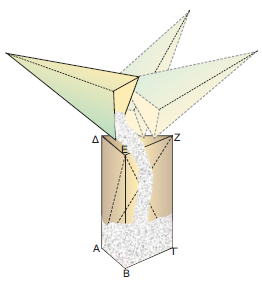
Όγκος πυραμίδας

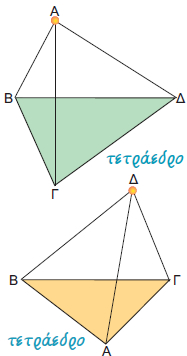
Κατασκευάζουμε με χαρτόνι ένα πρίσμα και μια πυραμίδα, έτσι ώστε να έχουν βάσεις ίσα τρίγωνα και ίσα ύψη. Αν γεμίσουμε διαδοχικά τρεις φορές με αλεύρι την πυραμίδα και αδειάσουμε το αλεύρι μέσα στο πρίσμα, θα δούμε ότι το πρίσμα γεμίζει τελείως. Η διαπίστωση αυτή ισχύει γενικότερα.

Επομένως, ο όγκος της πυραμίδας ισούται με το 1/3 του όγκου του πρίσματος.

Ο όγκος V της πυραμίδας ισούται με:

O ίδιος τύπος ισχύει για τον όγκο μιας πυραμίδας με βάση οποιοδήποτε πολύγωνο.

Μικροπείραμα

Μια κανονική πυραμίδα έχει βάση κανονικό δωδεκάγωνο με πλευρά 5 cm. Αν το ύψος μιας παράπλευρης έδρας της είναι 9 cm, να βρείτε το εμβαδόν της παράπλευρης επιφάνειάς της.

Λύση:

Μια κανονική τετραγωνική πυραμίδα έχει βάση με πλευρά 8 cm και ύψος 12 cm.

Να υπολογίσετε τον όγκο της.

Λύση:

Aπό έναν κύβο που έχει ακμή α = 10 cm, αφαιρούμε μια πυραμίδα, όπως φαίνεται στο παρακάτω σχήμα.

Να υπολογίσετε τον όγκο του στερεού που απομένει.

Λύση:

Μικροπείραμα

To έτος 3.000 π.Χ. περίπου οι αρχαίοι Αιγύπτιοι έκτισαν την πυραμίδα του Χέοπα, που έχει βάση τετράγωνο πλευράς 233 m και παράπλευρη ακμή 220 m (περίπου).

α) Να υπολογίσετε το εμβαδόν της παράπλευρης επιφάνειας αυτής της πυραμίδας.

β) Αν γνωρίζουμε ότι το ύψος της είναι 146 m, να υπολογίσετε τον όγκο της πυραμίδας.

Λύση:

ΣΩΣΤΟ

ΛΑΘΟΣ

Η τετραγωνική πυραμίδα και το τετράεδρο έχουν το ίδιο πλήθος εδρών.

Κάθε κανονική τριγωνική πυραμίδα είναι κανονικό τετράεδρο.

Στο παρακάτω σχήμα φαίνεται το ανάπτυγμα πυραμίδας.

O αριθμός των εδρών μιας πυραμίδας είναι πάντα άρτιος αριθμός.

Σε μια πυραμίδα το ύψος βρίσκεται πάνω στην παράπλευρη επιφάνεια.

Στο παρακάτω σχήμα, οι πυραμίδες ΙΕΖΗΘ και ΗΑΒΖΕ έχουν τον ίδιο όγκο.

Ο λόγος των όγκων μιας πυραμίδας και ενός πρίσματος με ίδια βάση και ίσα ύψη είναι:

Να κυκλώσετε τη σωστή απάντηση.

Οι παράπλευρες έδρες μιας κανονικής πυραμίδας είναι τρίγωνα:

A: Ισόπλευρα Β: Ισοσκελή Γ: Ορθογώνια Δ: Σκαληνά

Να κυκλώσετε τη σωστή απάντηση.

Η πυραμίδα του διπλανού σχήματος έχει βάση:

A: ΟΓΔ Β: ΟΒΓ Γ: ΑΒΓΔ Δ: ΟΑΒ

Να κυκλώσετε τη σωστή απάντηση.

1.	Να συμπληρώσετε τον παρακάτω πίνακα που αφορά στα στοιχεία μιας κανονικής τετραγωνικής πυραμίδας.
2.	Μια κανονική πυραμίδα έχει βάση τετράγωνο με πλευρά 12 cm και ύψος 10 cm. Να υπολογίσετε τον όγκο της.
3.	Μια κανονική εξαγωνική πυραμίδα έχει βάση με πλευρά 9 cm και απόστημα 12 cm. Να υπολογίσετε το εμβαδόν της παράπλευρης επιφάνειάς της.
4.	Μια κανονική πυραμίδα έχει βάση τετράγωνο πλευράς 9 cm και το ύψος της παράπλευρης έδρας της είναι 8 cm. Να υπολογίσετε το εμβαδόν: α) της παράπλευρης επιφάνειας, β) της ολικής επιφάνειας της πυραμίδας Μικροπείραμα
5.	Μια τετραγωνική πυραμίδα έχει όγκο 700 cm³ και ύψος 17 cm. Να υπολογίσετε την πλευρά του τετραγώνου της βάσης της.

6.	Μια κανονική τετραγωνική πυραμίδα έχει απόστημα 10 cm και πλευρά βάσης 16 cm. Να υπολογίσετε το εμβαδόν της παράπλευρης επιφάνειάς της και τον όγκο της.
7.	Ένα τετράεδρο έχει όλες τις ακμές του ίσες με 6 cm. Να υπολογίσετε το εμβαδόν της ολικής επιφάνειάς του.
8.	Ο όγκος μιας κανονικής τετραγωνικής πυραμίδας είναι εννεαπλάσιος από τον όγκο μίας άλλης κανονικής πυραμίδας με την οποία έχει το ίδιο ύψος. Να βρείτε το λόγο των πλευρών των βάσεών τους.
9.	Στο παρακάτω σχήμα φαίνεται ένας κύβος πλευράς α = 10 cm και μια πυραμίδα με βάση μία έδρα του κύβου και ύψος υ = 6 cm. Να υπολογίσετε τον όγκο του στερεού.
10.	Μια κανονική πυραμίδα με βάση εξάγωνο έχει ύψος 8 cm και παράπλευρη ακμή 10 cm. Να υπολογίσετε: α) το εμβαδόν της παράπλευρης επιφάνειας της πυραμίδας, β) το εμβαδόν της ολικής επιφάνειας της πυραμίδας, γ) τον όγκο της πυραμίδας.

Μικροπείραμα