|
Η έννοια του όγκου
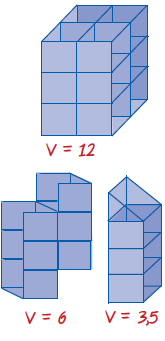
Ας θεωρήσουμε ένα στερεό σώμα Σ και έναν κύβο με ακμή μήκους μία μονάδα. Ο θετικός αριθμός που δηλώνει με πόσες επαναλήψεις του κύβου ή μέρους του κύβου σχηματίζεται το στερεό σώμα Σ, λέγεται όγκος του σώματος.
Moνάδες μέτρησης όγκου
Ως μονάδα μέτρησης όγκου θεωρούμε έναν κύβο με ακμή μήκους 1 μέτρο (m).
Ο όγκος του ισούται με 1 κυβικό μέτρο (m3).
Οι κυριότερες υποδιαιρέσεις του κυβικού μέτρου είναι:
| α) |
Το κυβικό δεκατόμετρο (dm3) που είναι όγκος κύβου με ακμή 1 dm.
Αφού 1m =10 dm, θα ισχύει ότι:
1 m3 = 103 dm3 = 1000 dm3.
Αντίστροφα ισχύει ότι:
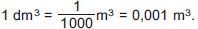 |
| β) |
Το κυβικό εκατοστόμετρο (cm3) που είναι όγκος κύβου με ακμή 1cm.
Ισχύει ότι 1 m = 10 dm = 100 cm, οπότε
1 m3 = 103 dm3 = 1003 cm3.
Αντίστροφα ισχύει ότι:
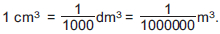 |
| γ) |
Το κυβικό χιλιοστόμετρο (mm3) που είναι όγκος κύβου με ακμή 1mm.
Ισχύει ότι 1 m = 10 dm = 100 cm= 1000 mm,
οπότε 1 m3 = 103 dm3 = 1003 cm3= 10003 mm3.
Αντίστροφα ισχύει ότι:

|
Στον όγκο των υγρών συνηθίζουμε να ονομάζουμε το dm3 ως λίτρο (ℓ ). Τότε, το cm3 λέγεται χιλιοστόλιτρο (mℓ).
Μικροπείραμα 
Όγκος πρίσματος και κυλίνδρου
Ας θεωρήσουμε μια σύριγγα γεμάτη χρωματισμένο νερό. Ασκώντας πίεση, το έμβολο διαγράφει το μήκος της σύριγγας έως ότου αδειάσει όλο το νερό.
Είναι φανερό ότι το νερό έχει όγκο ίσο με τον όγκο της κυλινδρικής σύριγγας.
Ο όγκος της σύριγγας διαγράφεται από την κίνηση του εμβαδού του εμβόλου σε όλο το μήκος της.
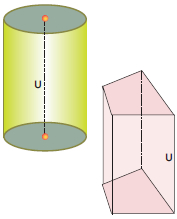
Ο όγκος ενός κυλίνδρου ισούται με το γινόμενο του εμβαδού της βάσης του επί το ύψος, δηλαδή:
Όγκος = (Εμβαδόν βάσης) • (ύψος) |
Είναι φανερό ότι το ίδιο θα ισχύει, αν στη θέση της κυλινδρικής σύριγγας έχουμε ένα οποιοδήποτε πρίσμα.
Ο όγκος ενός πρίσματος ισούται με το γινόμενο του εμβαδού της βάσης του επί το ύψος, δηλαδή:
Όγκος = (Εμβαδόν βάσης) • (ύψος) |
|
|
| 1 |
Να βρείτε τον όγκο του κυλίνδρου στις παρακάτω περιπτώσεις:
α) με ακτίνα βάσης 3 cm και ύψος 5 cm,
β) με διάμετρο βάσης 4 cm και ύψος 4 cm,
γ) με περίμετρο βάσης 31,4 cm και ύψος 3 cm. |
Λύση: |
α) Εφαρμόζουμε τον τύπο του όγκου V του κυλίνδρου και έχουμε:
V = πρ2 • υ = π • 32 • 5 = 45π = 141,3 (cm3).
β) Αφού η διάμετρος είναι δ = 4 cm, η ακτίνα είναι ρ = 2 cm.
Εφαρμόζουμε τον τύπο του όγκου κυλίνδρου και έχουμε:
V = πρ2 • υ = π • 22 • 4 = 16π = 50,24 (cm3).
γ) Πρώτα υπολογίζουμε την ακτίνα του κύκλου της βάσης:
L = 2πρ ή
31,4 = 2π • ρ ή
31,4 = 6,28 • ρ ή
ρ = 5 (cm).
Στη συνέχεια, εφαρμόζουμε τον τύπο του όγκου κυλίνδρου και έχουμε:
V = πρ2 • υ = π • 52 • 3 = 75π = 235,5 (cm3). |
| 2 |
Ο διπλανός κορμός δέντρου θεωρούμενος ως κύλινδρος έχει μήκος 8 m και διάμετρο βάσης 0,6 m. Η τιμή του συγκεκριμένου είδους ξυλείας είναι 100 € ανά κυβικό μέτρο. Πόσο αξίζει ο κορμός; |
 |
Λύση: |
Αφού η διάμετρος του κορμού είναι δ = 0,6 m, τότε η ακτίνα του κύκλου της βάσης του κυλίνδρου είναι ρ = 0,3 (m).
Επομένως, ο όγκος του κυλίνδρου είναι:
VK = πρ2 • υ = 3,14 • (0,3)2 • 8 = 2,26 (m3).
Αφού η αξία του συγκεκριμένου είδους ξυλείας είναι 100 € το κυβικό μέτρο, η αξία του κορμού είναι: Α = 2,26 • 100 = 226 €. |
| 3 |
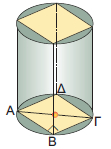
Ένα πρίσμα έχει βάση τετράγωνο πλευράς α (cm) και είναι εγγεγραμμένο σε κύλινδρο με ύψος 10 cm και ακτίνα βάσης ρ = 3 cm.
α) Να υπολογίσετε τη πλευρά α του τετραγώνου.
β) Να υπολογίσετε τον όγκο του κυλίνδρου και τον όγκο του πρίσματος. |
 |
Λύση: |
α) Το ορθογώνιο τρίγωνο ΑΒΓ έχει υποτείνουσα ΑΓ = 2 • ρ = 2• 3 = 6 (cm).
Από το Πυθαγόρειο θεώρημα έχουμε:
α2 + α2 = 62 ή 2α2 = 36 ή α2 = 18.
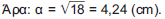
β) Ο όγκος του κυλίνδρου είναι: Vκυλ = πρ2υ = 3,14 • 32 • 10 = 282,6 (cm2).
O όγκος του πρίσματος είναι: Vπρ = Εβ • υ = α2 • υ = 18 • 10 = 180 (cm2). |
| |
1. |
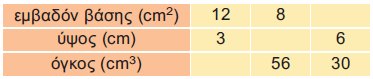
Να συμπληρώσετε τον παρακάτω πίνακα, όπου φαίνεται το εμβαδόν της βάσης, το ύψος και ο όγκος πρίσματος.
|
2. |
Να συμπληρώσετε τον παρακάτω πίνακα, όπου φαίνεται το εμβαδόν της βάσης, το ύψος και ο όγκος κυλίνδρου.

|
3. |
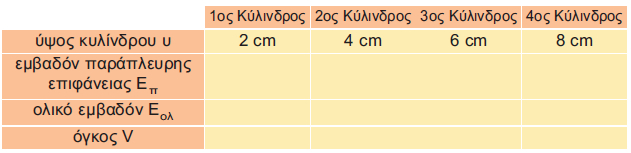
Δίνονται τέσσερις κύλινδροι που έχουν όλοι ακτίνα βάσης ρ=4 cm. Να συμπληρώσετε τον παρακάτω πίνακα:
|
Μικροπείραμα  |
| |
1. |
Τριγωνικό πρίσμα με βάση ορθογώνιο τρίγωνο ΑΒΓ με κάθετες πλευρές ΑΒ = 3 cm και ΑΓ = 4 cm έχει ύψος ίσο με την υποτείνουσα ΒΓ του τριγώνου ΑΒΓ.
Να υπολογίσετε:
α) το εμβαδόν της παράπλευρης επιφάνειας του πρίσματος,
β) το εμβαδόν της ολικής επιφάνειάς του,
γ) τον όγκο του πρίσματος.
|
2. |
Δίνεται πρίσμα με βάση ισόπλευρο τρίγωνο. Αν γνωρίζετε ότι το ύψος του είναι τετραπλάσιο από την πλευρά του ισόπλευρου τριγώνου της βάσης του και η παράπλευρη επιφάνειά του έχει εμβαδόν 432 cm2, να υπολογίσετε τον όγκο του. |
3. |
Ένα τετραγωνικό πρίσμα έχει ολικό εμβαδόν που είναι τριπλάσιο του εμβαδού της παράπλευρης επιφάνειάς του. Να αποδείξετε ότι η πλευρά του τετραγώνου της βάσης του είναι τετραπλάσια από το ύψος του πρίσματος. |
4. |
Ένα πρίσμα έχει βάση ισοσκελές τραπέζιο ΑΒΓΔ, με ίσες πλευρές ΑΔ = ΒΓ = 5 cm. Tο ύψος του τραπεζίου είναι 3 cm και το ύψος του πρίσματος είναι 10 cm. Αν ο όγκος του πρίσματος είναι 180 cm3 και το εμβαδόν της παράπλευρης επιφάνειας είναι 220 cm2,
να βρείτε:
α) το εμβαδόν και την περίμετρο του τραπεζίου ΑΒΓΔ,
β) τα μήκη των βάσεων ΑΒ και ΓΔ του τραπεζίου ΑΒΓΔ.
|
5. |
Λυγίζουμε ένα φύλλο χαρτιού μεγέθους Α4 (21x29cm) και κατασκευάζουμε έναν κύλινδρο ύψους 21cm. Nα βρείτε την ακτίνα βάσης και τον όγκο του κυλίνδρου. |
|
|
6. |
Να βρείτε τον όγκο κυλίνδρου ο οποίος έχει:
α) ακτίνα βάσης 10 cm και ύψος 1,2 cm.
β) εμβαδόν βάσης 100 mm2 και ύψος 0,2 m. |
7. |
Ένα τσιγάρο έχει μήκος 8,5 cm από τα οποία τα 2,5 cm καταλαμβάνει το φίλτρο. Η διάμετρος μιας βάσης του είναι 0,8 cm. Οι αναλύσεις του Υπουργείου Υγείας κατέληξαν στο συμπέρασμα ότι περιέχει 0,5 mg πίσσας ανά κυβικό εκατοστό καπνού και ότι το τσιγαρόχαρτο περιέχει 0,05 mg πίσσας ανά τετραγωνικό εκατοστό χαρτιού.
Πόσα mg πίσσας εισπνέει ημερησίως ένας καπνιστής που καπνίζει 15 τσιγάρα την ημέρα; (Να θεωρήσετε ότι ο καπνιστής πετάει το τσιγάρο έχοντας καπνίσει τα 5 από τα 6 cm του τσιγάρου).
|

|
|
|
|