B4.2: Στοιχεία και εμβαδόν πρίσματος και κυλίνδρου

4.2.	Στοιχεία και εμβαδόν πρίσματος και κυλίνδρου

Το ορθό πρίσμα και τα στοιχεία του

Στο φυσικό κόσμο τα αντικείμενα των διπλανών σχημάτων μάς δίνουν την έννοια του ορθού πρίσματος. Στη Στερεομετρία τα παρακάτω στερεά σώματα ονομάζονται ορθά πρίσματα. Στη συνέχεια, τα ορθά πρίσματα θα τα λέμε απλά πρίσματα.

Κάθε πρίσμα έχει:

δύο έδρες παράλληλες, που είναι ίσα πολύγωνα και τις άλλες έδρες του που είναι ορθογώνια παραλληλόγραμμα και ονομάζονται παράπλευρες έδρες.

Οι δύο παράλληλες έδρες του λέγονται βάσεις του πρίσματος.

Οι παράπλευρες έδρες σχηματίζουν την παράπλευρη επιφάνεια του πρίσματος. Οι πλευρές των εδρών του πρίσματος ονομάζονται ακμές.

Μικροπείραμα

Η απόσταση των δύο βάσεων, που είναι ίση με το ύψος μιας παράπλευρης έδρας, λέγεται ύψος του πρίσματος.

Αν οι βάσεις του πρίσματος είναι τρίγωνο, τετράπλευρο, πεντάγωνο κ.ο.κ, τότε αντίστοιχα το πρίσμα λέγεται τριγωνικό, τετραπλευρικό, πενταγωνικό κ.ο.κ.

Δύο από τα βασικότερα ορθά πρίσματα είναι ο κύβος και το ορθογώνιο παραλληλεπίπεδο.

Μικροπείραμα Μικροπείραμα Μικροπείραμα Μικροπείραμα

Εμβαδόν επιφάνειας πρίσματος

Στο παρακάτω σχήμα βλέπουμε τη διαδικασία ανάπτυξης και το τελικό ανάπτυγμα της επιφάνειας ενός πρίσματος. Ως ανάπτυγμα της επιφάνειας ενός πρίσματος θεωρούμε το επίπεδο σχήμα που προκύπτει αν «ξεδιπλώσουμε» την παράπλευρη επιφάνειά του και τις βάσεις του.

Η παράπλευρη επιφάνεια σχηματίζει ένα ορθογώνιο, που η μία διάστασή του είναι η περίμετρος της βάσης και η άλλη το ύψος του πρίσματος.

Το εμβαδόν της παράπλευρης επιφάνειας ενός πρίσματος ισούται με το γινόμενο της περιμέτρου της βάσης του επί το ύψος του πρίσματος. Δηλαδή:

Ε_π = (περίμετρος βάσης) • (ύψος)

Φυσικά, για να βρούμε το ολικό εμβαδόν, πρέπει να προσθέσουμε και τα εμβαδά των δύο βάσεων.

Το ολικό εμβαδόν ενός πρίσματος (Ε_ολ) είναι το άθροισμα του εμβαδού της παράπλευρης επιφάνειας Ε_π και των εμβαδών Ε_β των δύο βάσεων. Δηλαδή:

Ε_ολ = Ε_π+ 2Ε_β

Μικροπείραμα Μικροπείραμα Μικροπείραμα Μικροπείραμα

Κύλινδρος

Τα παρακάτω στερεά δίνουν την έννοια του κυλίνδρου.

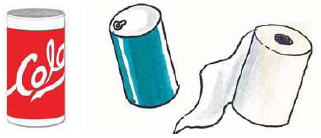
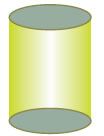
Ένας κύλινδρος αποτελείται από δύο ίσους και παράλληλους κυκλικούς δίσκους, που είναι οι βάσεις του, και την παράπλευρη επιφάνεια, που, αν την ξετυλίξουμε, θα δούμε ότι έχει σχήμα ορθογωνίου.

Η απόσταση των δύο βάσεων λέγεται ύψος του κυλίνδρου.

Μικροπείραμα

Εμβαδόν επιφάνειας κυλίνδρου

Ας θεωρήσουμε το ανάπτυγμα ενός κυλίνδρου. Είναι φανερό ότι το εμβαδόν της παράπλευρης επιφάνειας του κυλίνδρου ισούται με το εμβαδόν του ορθογωνίου που σχηματίζεται, οπότε ισούται με το γινόμενο της περιμέτρου της βάσης επί το ύψος του κυλίνδρου.

Η περίμετρος της βάσης ισούται με το μήκος του κύκλου, δηλαδή 2πρ.

Το εμβαδόν Ε_π της παράπλευρης επιφάνειας ενός κυλίνδρου ισούται με την περίμετρο της βάσης (που είναι ίση με 2πρ) επί το ύψος του κυλίνδρου. Δηλαδή

Ε_π = (περίμετρος βάσης) • (ύψος) ή Ε_π =2πρ • υ

Φυσικά, για να βρούμε το ολικό εμβαδόν του κυλίνδρου, πρέπει στο εμβαδόν της παράπλευρης επιφάνειας να προσθέσουμε τα εμβαδά των δύο βάσεων.

Το ολικό εμβαδόν Ε_ολ ενός κυλίνδρου ισούται με το εμβαδόν της παράπλευρης επιφάνειας Ε_π και τα εμβαδά Ε_β των δύο βάσεων. Δηλαδή:

Ε_ολ = Ε_π+ 2Ε_β

1
Να βρείτε πόσο χαρτόνι (σε cm²) χρειάζεται, για να κατασκευαστεί το πρίσμα του παρακάτω σχήματος, του οποίου οι βάσεις είναι ορθογώνια τρίγωνα με κάθετες πλευρές 3 cm και 4 cm αντίστοιχα και το ύψος είναι 10 cm.

Λύση:

Μικροπείραμα

2
Να υπολογιστεί το εμβαδόν της παράπλευρης επιφάνειας του πρίσματος που δίνεται στο διπλανό σχήμα.

Λύση:

Οι βάσεις του πρίσματος είναι τετράπλευρα με περίμετρο:

3 + 4 + 6 + 5 = 18 (cm).

Το ύψος του πρίσματος είναι 7 cm. Άρα, το εμβαδόν της παράπλευρης επιφάνειας είναι:

Ε_π = (περίμετρος βάσης) • (ύψος) = 18 • 7 = 126 (cm²).

Κόστος δεξαμενής καυσίμων

Μια κλειστή δεξαμενή αποθήκευσης καυσίμων έχει σχήμα κυλίνδρου με ύψος 20 m και ακτίνα βάσης ρ = 30 m. Είναι κατασκευασμένη από ειδική λαμαρίνα που κοστίζει 5 € το τετραγωνικό μέτρο.

Ποιο είναι το κόστος της λαμαρίνας για την κατασκευή της δεξαμενής;

Λύση:

Πρέπει να βρούμε πόσα τετραγωνικά μέτρα λαμαρίνας χρησιμοποιήθηκαν (δηλαδή το ολικό εμβαδόν) και να το πολλαπλασιάσουμε με το κόστος 5 € ανά τετραγωνικό μέτρο.

Η παράπλευρη επιφάνεια έχει εμβαδόν:
Ε_π = (περίμετρος βάσης) • (ύψος) = 2πρ • υ = 2 • 3,14 • 30 • 20 = 3768 (m²).
Καθεμία από τις βάσεις έχει εμβαδόν: Ε_β = πρ² = 3,14 • 30² = 2826 (m²).
Το ολικό εμβαδόν του κυλίνδρου είναι:
Ε_ολ = Ε_π + 2 • Ε_β = 3768 + 2 • 2826 = 9420 (m²).

Επομένως, το κόστος της λαμαρίνας είναι 9420 • 5 = 47100 €.

Μικροπείραμα

Η βάση της μηχανής

Το διπλανό κλειστό κουτί κατασκευάζεται από ξύλο και χρησιμεύει ως βάση μιας μηχανής. Να βρείτε την επιφάνεια του ξύλου που θα χρησιμοποιηθεί για την κατασκευή της βάσης.

Λύση:

Παρατηρούμε ότι το κουτί είναι ένα πενταγωνικό πρίσμα με βάσεις τα πεντάγωνα

ΑΒΓΔΕ και ΖΗΘΙΚ.

Η περίμετρος της κάθε βάσης είναι: ΑΒ + ΒΓ + ΓΔ + ΔΕ + ΕΑ = 20 + 4 + 10 + 12 + 10 = 56 (cm).

Το ύψος του πρίσματος είναι υ = ΑΖ = 5 (cm).

Επομένως, το εμβαδόν της παράπλευρης επιφάνειας είναι:

Ε_π = (περίμετρος βάσης) • (ύψος) = 56 • 5 = 280 (cm²).

Για να βρούμε το εμβαδόν της βάσης ΑΒΓΔΕ, τη χωρίζουμε σε δύο μέρη: σε ένα ορθογώνιο ΑΕΔΔ' και σε ένα τραπέζιο ΒΓΔΔ'.

Το εμβαδόν του ορθογωνίου ΑΕΔΔ' είναι ίσο με 10 • 12 = 120 (cm²). Το εμβαδόν του τραπεζίου ΒΓΔΔ' είναι ίσο με:

Άρα, το εμβαδόν της βάσης είναι: Ε_β = 120 + 56 = 176 (cm²). Τ

ο ολικό εμβαδόν του πρίσματος είναι: Ε_ολ = Ε_π + 2Ε_β = 280 + 2 • 176 = 280 + 352 = 632 (cm²).

Να κυκλώσετε τη σωστή απάντηση σε καθεμιά από τις παρακάτω προτάσεις.

Ένα πρίσμα με βάση πεντάγωνο έχει:

α) A: 5 έδρες Β: 6 έδρες Γ: 7 έδρες.

β) A: 8 κορυφές Β: 10 κορυφές Γ: 12 κορυφές.

γ) A: 10 ακμές Β: 15 ακμές Γ: 12 ακμές.

Δίνεται πρίσμα με βάση τετράγωνο πλευράς 10cm και ύψους 8cm.

α) Το εμβαδόν της παράπλευρης επιφάνειάς του είναι:

A: 400 cm² Β: 320 cm² Γ: 800 cm².

β) Το ολικό εμβαδόν του είναι:

A: 600 cm² Β: 520 cm² Γ: 800 cm².

Ένας κύλινδρος έχει διάμετρο βάσης 10cm και ύψος 8cm.

α) Το εμβαδόν της παράπλευρης επιφάνειάς του είναι:

A: 40π cm² Β: 60π cm² Γ: 80π cm².

β) Το ολικό εμβαδόν του είναι:

A: 100π cm² Β: 110π cm² Γ: 130π cm².

1.	Να συμπληρώσετε τον παρακάτω πίνακα, όπου φαίνεται η περίμετρος της βάσης, το ύψος και το εμβαδόν της παράπλευρης επιφάνειας πρίσματος.
2.	Να βρείτε το εμβαδόν της παράπλευρης επιφάνειας τριγωνικού πρίσματος του οποίου η βάση είναι τρίγωνο με πλευρές α = 3 dm, β = 5 dm, γ = 6 dm και το ύψος 0,8 cm.
3.	Έστω α, β, γ τα μήκη των πλευρών της βάσης ενός τριγωνικού πρίσματος, υ το ύψος του και Επ το εμβαδόν της παράπλευρης επιφάνειας. Να συμπληρώσετε τον παρακάτω πίνακα.
4.	Θέλουμε να βάψουμε τους τοίχους ενός δωματίου που έχει σχήμα ορθογωνίου παραλληλεπιπέδου με διαστάσεις: πλάτος 4 m, μήκος 5 m και ύψος 3 m. Πόσα κιλά χρώμα πρέπει να αγοράσουμε, αν είναι γνωστό ότι ένα κιλό χρώματος καλύπτει περίπου 9 m²;
5.	Nα υπολογίσετε το ολικό εμβαδόν πρίσματος με ύψος υ = 20 cm και βάσεις ισόπλευρα τρίγωνα πλευράς 4 cm.
6.	H σκηνή ενός κάμπινγκ είναι κατασκευασμένη από ύφασμα (μαζί με το δάπεδό της) και έχει διαστάσεις που φαίνονται στο παρακάτω σχήμα. Πόσα τετραγωνικά μέτρα ύφασμα χρειάστηκαν για την κατασκευή της;

7.	Να βρεθεί το εμβαδόν της παράπλευρης επιφάνειας και το ολικό εμβαδόν ενός κυλίνδρου, όταν: α) Έχει ακτίνα βάσης 3 cm και ύψος 5 cm. β) Έχει διάμετρο βάσης 4 cm και ύψος 6 cm. γ) Έχει περίμετρο βάσης 15,7 cm και ύψος 32 cm. δ) Έχει εμβαδόν βάσης 50,24 cm² και ύψος 2 dm.
8.	Να συμπληρώσετε τον παρακάτω πίνακα που συνδέει την ακτίνα της βάσης και το ύψος ενός κυλίνδρου με το εμβαδόν της παράπλευρης επιφάνειας και το ολικό εμβαδόν του.
9.	Το κυλινδρικό κουτί μιας κονσέρβας έχει ύψος 12 cm και ακτίνα βάσης 3 cm. Το υλικό των βάσεων κοστίζει 0,5 € το τετραγωνικό μέτρο, ενώ το υλικό της παράπλευρης επιφάνειας κοστίζει 0,3 € το τετραγωνικό μέτρο. Πόσο θα κοστίζει το υλικό όταν πρόκειται να κατασκευάσουμε 1000 κουτιά;