
|
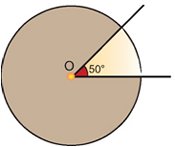
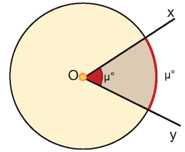
Ας θεωρήσουμε ένα κύκλο (Ο, ρ) και μια επίκεντρη γωνία $x\hat{O}y$ μέτρου μ°.
Το μέρος του κυκλικού δίσκου που περιέχεται μέσα στη γωνία $x\hat{O}y$ λέγεται κυκλικός τομέας γωνίας μ° του κύκλου (Ο, ρ).
|
|
Av η επίκεντρη γωνία $x\hat{O}y$ είναι μέτρου μ°, τότε και το αντίστοιχο τόξο της έχει μέτρο μ°, οπότε βρίσκουμε το εμβαδόν του κυκλικού τομέα:

|
| Τόξο σε μοίρες |
360° |
μ° |
| Εμβαδόν |
πρ² |
Ε |
|
Αν το τόξο έχει μετρηθεί σε ακτίνια και ισούται με α rad, τότε πάλι έχουμε:
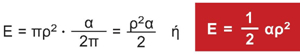
|
Τόξο σε ακτίνια (rad) |
2π |
α |
Εμβαδόν |
πρ² |
Ε |
|
Μικροπείραμα 
| 1 |
Μια κυκλική πλατεία έχει ακτίνα ρ = 20 m. Ένας προβολέας είναι τοποθετημένος στο κέντρο της πλατείας και εκπέμπει μια δέσμη φωτός που φωτίζει ένα κυκλικό τομέα γωνίας 50°.
α) Να βρείτε το εμβαδόν της πλατείας.
β) Να βρείτε το εμβαδόν του κυκλικού τομέα που φωτίζεται. |
Λύση
α) Το εμβαδόν της πλατείας είναι: Ε = πρ² = 3,14 • 20² = 1256 (m²).
β) Γνωρίζουμε ότι όλη η πλατεία αντιστοιχεί σε τόξο 360° και έχει εμβαδόν 1256 m². Για να βρούμε το εμβαδόν ε του κυκλικού τομέα που αντιστοιχεί σε τόξο 50°, χρησιμοποιούμε την απλή μέθοδο των τριών, οπότε :
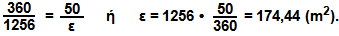
|
|
|
|
| 1 |
| Να υπολογίσετε το εμβαδόν του κυκλικού τομέα στον στίβο της σφαιροβολίας ακτίνας ρ = 24 m και γωνίας 65°. |
 |
Λύση: |
Το εμβαδόν του κυκλικού τομέα δίνεται από τον τύπο:
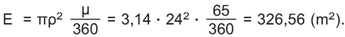
|
| 2 |
O παρακάτω κύκλος έχει διάμετρο ΑΒ και εμβαδόν 40 cm².
Να υπολογίσετε τα εμβαδά Ε1, Ε2, Ε3, Ε4. |
Λύση: |
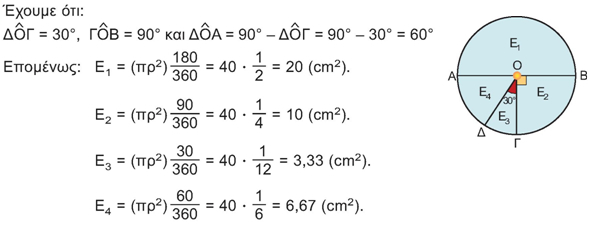
|
| |
1. |
Να συμπληρώσετε τον παρακάτω πίνακα: |
|
ακτίνα κύκλου |
γωνία κυκλικού τομέα |
εμβαδόν κυκλικού τομέα |
ρ = 2 cm |
μ = 60° |
|
|
μ = 45° |
Ε = 8π cm² |
ρ = 3 cm |
|
Ε = 3π cm² |
2. |
Σ' έναν κύκλο κέντρου Ο και ακτίνας ρ =.................. (cm) ο κυκλικός τομέας γωνίας 120°
έχει μήκος τόξου 6π (cm) και εμβαδόν .....................(cm²).
Να συμπληρώσετε τα κενά. |
3. |
Η ακτίνα ενός κύκλου είναι 12 cm. Ένας κυκλικός τομέας γωνίας 60° έχει εμβαδόν:
Α: 24π (cm²) B: 36π (cm²) Γ: 54π (cm²) Δ: 108π (cm²).
Να κυκλώσετε τη σωστή απάντηση. |
4. |
Αν το εμβαδόν κυκλικού τομέα είναι 12,56 cm² και η γωνία του είναι 90°, η ακτίνα του κύκλου είναι:
Α: 2 cm Β: 4 cm, Γ: 9 cm, Δ: 7 cm.
Να κυκλώσετε τη σωστή απάντηση. |
5. |
Αν τριπλασιάσουμε την ακτίνα ενός κύκλου (Ο, ρ), τότε το εμβαδόν ενός κυκλικού τομέα του κύκλου:
Α: διπλασιάζεται Β: τριπλασιάζεται Γ: εξαπλασιάζεται Δ: εννιαπλασιάζεται.
Να κυκλώσετε τη σωστή απάντηση. |
|
| |
1. |
Να υπολογιστεί η γωνία κυκλικού τομέα που έχει εμβαδόν ίσο με το 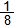 του εμβαδού του κύκλου. του εμβαδού του κύκλου. |
2. |
Ένας κυκλικός τομέας γωνίας 30° έχει εμβαδόν 1 m².
Να υπολογίσετε την ακτίνα του κύκλου. |
3. |
Το εμβαδόν ενός κυκλικού δίσκου είναι 1256 cm².
Να υπολογίσετε το εμβαδόν ενός κυκλικού τομέα γωνίας 36°. |
4. |
Το εμβαδόν κυκλικού τομέα γωνίας 45° είναι 20,25π cm².
Να βρείτε το εμβαδόν του κύκλου στον οποίο ανήκει ο τομέας. |
5. |
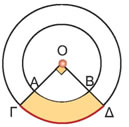
Δύο ομόκεντροι κύκλοι έχουν ακτίνες ρ1=3 cm και ρ2=4 cm αντίστοιχα.
Να υπολογίσετε το εμβαδόν του γραμμοσκιασμένου μέρους του σχήματος.
|
6. |
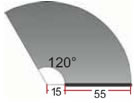
Ο υαλοκαθαριστήρας ενός αυτοκινήτου έχει μήκος 55 cm. Το σημείο περιστροφής απέχει από το λάστιχο καθαρισμού 15 cm. Αν ο υαλοκαθαριστήρας διαγράφει γωνία 120°, να υπολογίσετε την επιφάνεια που καθαρίζει.
Μικροπείραμα  |
|
|
7. |
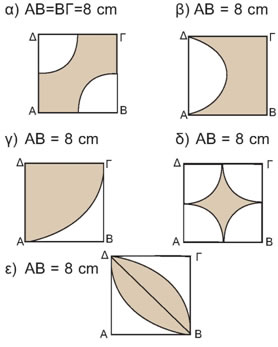
Να υπολογίσετε τα εμβαδά των γραμμοσκιασμένων καμπυλόγραμμων επιφανειών στα παρακάτω τετράγωνα:
Μικροπείραμα  Μικροπείραμα Μικροπείραμα 
|
8. |
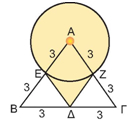
Να βρείτε το εμβαδόν της γραμμοσκιασμένης επιφάνειας στο σχήμα, αν οι αριθμοί εκφράζουν τα μήκη των αντίστοιχων τμημάτων σε cm.
|
|
|
|