|
| 1 |
Ας θεωρήσουμε ένα νόμισμα των 2 €. Αφού μετρήσετε τη διάμετρό του δ, να βάλετε μελάνι γύρω - γύρω από το νόμισμα και να το κυλίσετε κάθετα στο χαρτί, έτσι ώστε να κάνει μια πλήρη περιστροφή.
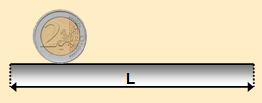
α) Το μήκος L που διαγράφει είναι το μήκος του κύκλου.
Συμπληρώστε τον παρακάτω πίνακα:
β) Ας δούμε κατόπιν μερικές προσεγγιστικές μετρήσεις από την Αστρονομία για την «περιφέρεια» και τις διαμέτρους κάποιων πλανητών.
Συμπληρώστε τον πίνακα:
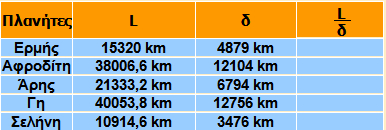
Να κάνετε τις πράξεις με ακρίβεια δύο δεκαδικών ψηφίων χρησιμοποιώντας έναν υπολογιστή τσέπης.
Τι παρατηρείτε; |
Λύση
α) Έχουμε ότι:
β) Παρατηρούμε ότι ο λόγος 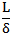 είναι περίπου 3,14 για όλους τους πλανήτες.
Αυτός ο σταθερός λόγος ονομάστηκε από τους αρχαίους Έλληνες ως «ο αριθμός π», ο πιο διάσημος και αξιοσημείωτος απ' όλους τους αριθμούς (βλέπε Ιστορικό σημείωμα).
Αποδεικνύεται ότι ο αριθμός π είναι ένας άρρητος αριθμός, δηλαδή δεκαδικός με άπειρα ψηφία, τα οποία δεν προκύπτουν με συγκεκριμένη διαδικασία. Τα πρώτα 40 δεκαδικά ψηφία του π είναι:
π = 3,14159 26535 89793 23846 2643383279 50288 41971 ...
Από τη σχέση $\dfrac{L}{δ} = π$, προκύπτει ότι:
Το μήκος του κύκλου υπολογίζεται από τη σχέση:
|
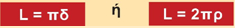
Παρατήρηση:
Στις εφαρμογές και ασκήσεις θα χρησιμοποιούμε για τον π την προσεγγιστική τιμή 3,14.
Μικροπείραμα  Μικροπείραμα Μικροπείραμα |
|
| 1 |
Ένας κύκλος έχει μήκος L = 9,42 cm. Να βρείτε το μήκος της ακτίνας του. |
Λύση: |
Για το μήκος του κύκλου ισχύει ότι:
|
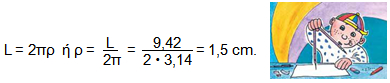
| 2 |
Ένας κύκλος έχει μήκος 10 cm περισσότερο από έναν άλλο. Πόσο μεγαλύτερη είναι η ακτίνα του; |
Λύση: |
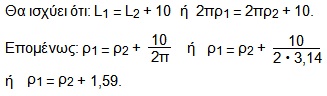
Δηλαδή, η ακτίνα του πρώτου κύκλου είναι μεγαλύτερη κατά 1,59 cm της ακτίνας του δεύτερου. |
| 3 |
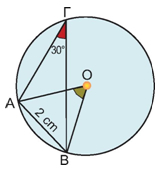
Να υπολογιστεί το μήκος του κύκλου στο παρακάτω σχήμα. |
Λύση: |
Η εγγεγραμμένη γωνία  είναι ίση με 30°, οπότε βρίσκουμε την αντίστοιχη επίκεντρη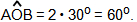 
Επομένως, το τρίγωνο ΑΟΒ είναι ισόπλευρο με ΟΑ = ΟΒ = ΑΒ = 2 cm, οπότε ρ = 2 cm.
Άρα, το μήκος του κύκλου είναι: L = 2πρ = 2 • 3,14 • 2 = 12,56 cm. |
 |
| |
1. |
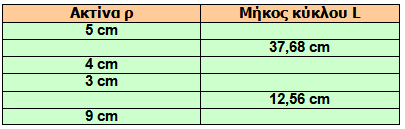
Να συμπληρώσετε τον παρακάτω πίνακα:
|
2. |
Αν τριπλασιάσουμε την ακτίνα ενός κύκλου (Ο, ρ), τότε το μήκος του κύκλου:
Α: διπλασιάζεται
Β: τριπλασιάζεται
Γ: τετραπλασιάζεται
Δ: παραμένει το ίδιο.
Να κυκλώσετε τη σωστή απάντηση. |
3. |
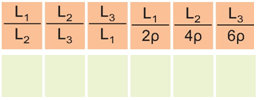
Τρεις ομόκεντροι κύκλοι έχουν ακτίνες ρ, 2ρ, 3ρ αντίστοιχα. Να συμπληρώσετε τον πίνακα:
|
|
|
| |
1. |
Ένας κύκλος έχει μήκος 20 cm περισσότερο από έναν άλλο. Πόσο μεγαλύτερη είναι η ακτίνα του; |
2. |
Γύρω από τον κορμό ενός αιωνόβιου δέντρου τυλίγουμε ένα σκοινί. Μετράμε το σκοινί και βρίσκουμε ότι έχει μήκος 3,5 m. Να υπολογίσετε την ακτίνα του κορμού.
|
3. |
Οι διάμετροι δύο κύκλων διαφέρουν κατά 5 cm.
Να βρείτε πόσο διαφέρουν:
α) οι ακτίνες τους
β) οι περίμετροί τους. |
4. |
Οι περίμετροι δύο κύκλων έχουν λόγο 2 προς 1.
Να βρείτε το λόγο:
α) των διαμέτρων τους.
β) των ακτίνων τους. |
|
|
5. |
Ο λεπτοδείκτης ενός ρολογιού έχει μήκος 2,5 cm. Να βρείτε πόσο διάστημα
θα διαγράψει το άκρο του λεπτοδείκτη σε 12 ώρες. |
6. |
Στη μηχανή ενός αυτοκινήτου δύο τροχαλίες Α, Β συνδέονται με ελαστικό ιμάντα. Αν ρΑ = 2 cm και ρB = 8 cm, να βρείτε πόσες στροφές θα κάνει η Α, αν η Β κάνει μία στροφή.
Μικροπείραμα |
7. |
Ένας ποδηλάτης, που προετοιμάζεται για τους αγώνες, προπονείται σε στίβο σχήματος κύκλου με ακτίνα ρ = 30 m. Πόσες στροφές θα κάνει σε 3 ώρες προπόνησης, αν κινείται με ταχύτητα 20km/h;
|
8. |
Γνωρίζουμε ότι ο Ισημερινός της Γης έχει μήκος 40.000 km περίπου. Θεωρώντας ότι η Γη είναι σφαιρική να βρείτε την ακτίνα της.
Μικροπείραμα |
|
|
π = 3,14159 26535 89793 23846 26433 83279 50288 41971... |
0 π είναι ο μόνος άρρητος και υπερβατικός, -όπως λέγεται- αριθμός που συναντάται στη φύση.
Στην Παλαιά Διαθήκη φαίνεται ότι ο π θεωρούνταν ίσος με το 3.
Οι Βαβυλώνιοι περίπου το 2.000 π.Χ. θεωρούσαν ότι ο π είτε είναι ίσος με το 3 είτε με το $3 \dfrac{1}{8}$.
Οι Αιγύπτιοι στον πάπυρο του Rhind (1500 π.Χ.) θεωρούσαν ότι το εμβαδόν ενός κύκλου ισούται με $\left(\dfrac{8}{9}δ\right)^2$, όπου δ η διάμετρος του κύκλου, οπότε, π ≈ 3,16049...
Ωστόσο, οι αρχαίοι Έλληνες ξέφυγαν από τις «χονδρικές» εκτιμήσεις των Βαβυλωνίων και των Αιγυπτίων και έδωσαν επιστημονική μέθοδο για τον υπολογισμό του π. Το συνδύασαν με ένα από τα περίφημα «άλυτα» προβλήματα της Αρχαιότητας: με το πρόβλημα του τετραγωνισμού του κύκλου, δηλαδή την κατασκευή με κανόνα και διαβήτη τετραγώνου ισεμβαδικού με δοσμένο κύκλο.
|
Εκτιμήσεις του π |
| Πολλοί επιστήμονες από την αρχαιότητα (με πρωτόγονα μέσα) μέχρι σήμερα (με σύγχρονους υπερυπολογιστές), προσπάθησαν να βρουν προσεγγίσεις του π με όσο το δυνατόν περισσότερα δεκαδικά ψηφία. Μερικές από αυτές τις προσπάθειες είναι οι παρακάτω: |
 |
|
|
