Μαθηματικά (B' Γυμνασίου) - Βιβλίο Μαθητή (Εμπλουτισμένο)
2.4. Οι τριγωνομετρικοί αριθμοί των γωνιών 30°, 45° και 60°

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Οι τριγωνομετρικοί αριθμοί της γωνίας 45ο

1

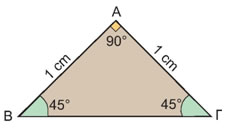
Ας θεωρήσουμε ένα ορθογώνιο και ισοσκελές τρίγωνο ΑΒΓ με κάθετες πλευρές ΑΒ = ΑΓ = 1 cm. Τότε οι γωνίες της βάσης του είναι $\hat{Β} = \hat{Γ} =$ 45o.

Να υπολογίσετε τους τριγωνομετρικούς αριθμούς ημ45°, συν45° και εφ45°.

Λύση

Από το Πυθαγόρειο θεώρημα έχουμε:

 

Οι τριγωνομετρικοί αριθμοί των γωνιών 30° και 60°

 

2

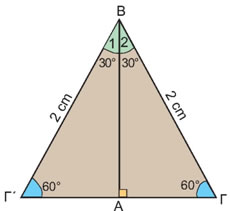
Ας θεωρήσουμε τώρα δύο ίσα ορθογώνια τρίγωνα ΑΒΓ και ΑΒΓ΄ με κοινή πλευρά την ΑΒ, οξείες γωνίες

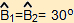και υποτείνουσες ΒΓ = ΒΓ' = 2 cm, όπως φαίνεται στο παρακάτω σχήμα. Να υπολογίσετε τους τριγωνομετρικούς αριθμούς ημ30°, συν30°, εφ30°, ημ60°, συν60° και εφ60°.

 

Λύση

Το τρίγωνο ΒΓΓ' είναι ισόπλευρο, αφού όλες οι γωνίες του είναι 60°, οπότε: ΓΓ' = 2 cm και ΑΓ = ΑΓ' = 1 cm.

Από το ορθογώνιο τρίγωνο ΑΒΓ έχουμε ότι:

Επίσης, στο ίδιο σχήμα μπορούμε να υπολογίσουμε το ημίτονο, το συνημίτονο και την εφαπτομένη της γωνίας

 

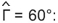
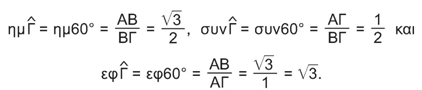
Σύμφωνα, λοιπόν, με τα παραπάνω έχουμε τον πίνακα:

 

 

Μικροπείραμα Πείραμα
1

Να αποδείξετε ότι ισχύει η ισότητα: ημ²45° = 1 – ημ30°.

 

Λύση:

 

2

Να αποδείξετε ότι το ύψος και το εμβαδόν ενός ισόπλευρου τριγώνου ΑΒΓ πλευράς α, δίνονται από τους τύπους:

 

Λύση:

 

3
Να υπολογιστεί η τιμή της παράστασης: Α = ημ30° + συν60° + 2συν30° - 2εφ45° + 2ημ45°.

 

Λύση:

Έχουμε: Α = ημ30° + συν60° + 2συν30° - 2εφ45° + 2ημ45°

 

 

 

 1.

Σε κάθε αριθμό της στήλης Α να αντιστοιχίσετε τον ίσο του αριθμό που βρίσκεται στη στήλη Β.

 2.

Αν ημθ = συνθ, όπου θ οξεία γωνία, τότε:

Α: θ = 30°     Β: θ = 45°     Γ: θ = 60°     Δ: θ = 90°

Να κυκλώσετε τη σωστή απάντηση.

 3.

Να χαρακτηρίσετε τις παρακάτω προτάσεις με Σ (σωστή) ή Λ (λανθασμένη):

α) ημ60° = 2ημ30°

β) 2συν60° = 1

γ) ημ45° + συν45° = 2ημ45°

δ) συν30° = ημ60°

ε) συν60° = ημ30°

 4.

Στο διπλανό κύβο για τη γωνία $θ = Β\hat{Α}Γ$ ισχύει ότι:

 

 

 

 1.

Να υπολογίσετε τις πλευρές α και β ενός ορθογωνίου τριγώνου ΑΒΓ στις παρακάτω περιπτώσεις:

 2.

Δίνεται τρίγωνο ΑΒΓ με πλευρές ΑΒ = 12 cm, ΒΓ = 5 cm, ΑΓ = 13 cm.

α) Να αποδείξετε ότι το τρίγωνο είναι ορθογώνιο.

β) Να υπολογίσετε το

Μικροπείραμα Πείραμα

 3.

Nα αποδείξετε τις παρακάτω ισότητες:

 4.

Να βρείτε την τιμή της παράστασης Α = 2ημ²ω - συνω στις παρακάτω περιπτώσεις:

α) ω = 30°

β) ω = 45°

γ) ω = 60°

 5.

Ένα αεροπλάνο Α πετά σε ύψος 1500m και φαίνεται από τον πύργο ελέγχου του αεροδρομίου με γωνία 30°. Ποια είναι η οριζόντια απόσταση ΠΒ από τον πύργο ελέγχου;

Μικροπείραμα Πείραμα

 6.

Στο παρακάτω σχήμα να υπολογίσετε τις αποστάσεις ΑΒ και ΑΔ.

 7.

Να υπολογίσετε το συνολικό μήκος της τεθλασμένης γραμμής ΑΒΓΔ στο παρακάτω σχήμα.

 8.

Στο παρακάτω σχήμα το σημείο Γ είναι μέσο του ΑΒ.

Να υπολογίσετε:

α) τη γωνία θ

β) την απόσταση ΑΕ

γ) την απόσταση ΕΔ

 9.

Να υπολογίσετε την περίμετρο του σχήματος.

 10.

Στο παρακάτω τραπέζιο ΑΒΓΔ να υπολογίσετε το μήκος της μεγάλης βάσης ΓΔ.

 11.

Σε μια ρώγα από σταφύλι...

Δύο σπουργίτια βρίσκονται στην κορυφή δύο στύλων ύψους 5 m και 9 m αντίστοιχα, όπως φαίνεται στο παρακάτω σχήμα. Ξεκινούν την ίδια στιγμή και με την ίδια ταχύτητα με στόχο μια ρώγα από σταφύλι που βλέπουν υπό γωνίες 60° και 30° στο έδαφος στο σημείο Ρ. Ποιο από τα δύο σπουργίτια θα φτάσει πρώτο τη ρώγα;

 12.

Για ν' ανέβουμε στον 2ο όροφο ενός εμπορικού κέντρου χρησιμοποιούμε τις κυλιόμενες σκάλες, όπως βλέπουμε στο σχήμα. Να υπολογίσετε το ύψος του 2ου ορόφου από το έδαφος.

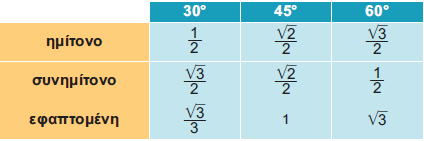
Μικροπείραμα Πείραμα