2.2.	Ημίτονο και συνημίτονο οξείας γωνίας

Το ημίτονο

Ένα πυροσβεστικό όχημα σταματά μπροστά από ένα κτίριο που φλέγεται, για να κατεβάσει έναν άνθρωπο που βρίσκεται στην ταράτσα του κτιρίου. Η σκάλα του οχήματος έχει μήκος ΟΑ = 50 m και το κτίριο έχει ύψος ΑΔ = 30 m. Ο πυροσβέστης που βρίσκεται στην άκρη της σκάλας παίρνει τον άνθρωπο που κινδυνεύει και η σκάλα αρχίζει να μαζεύεται. Να συμπληρώσετε τον παρακάτω πίνακα:

Τι παρατηρείτε;

Λύση

Παρατηρούμε ότι οι λόγοι της τρίτης στήλης παραμένουν σταθεροί:

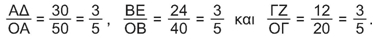
Είναι φανερό ότι ο λόγος αυτός παραμένει σταθερός για κάθε διαδοχική θέση της σκάλας. Επίσης, είναι φανερό ότι η γωνία ω στα ορθογώνια τρίγωνα ΟΑΔ, ΟΒΕ, ΟΓΖ που σχηματίζονται, παραμένει σταθερή.

Ο σταθερός αυτός λόγος γράφεται ως :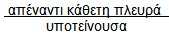

ονομάζεται ημίτονο της γωνίας ω και συμβολίζεται με ημω. Δηλαδή

Επομένως:

Ο λόγος που σχηματίζεται, αν διαιρέσουμε την απέναντι κάθετη πλευρά μίας οξείας γωνίας ω ενός ορθογωνίου τριγώνου με την υποτείνουσα, είναι πάντοτε σταθερός και λέγεται ημίτονο της γωνίας ω.

Μικροπείραμα

Το συνημίτονο

Αν συμπληρώσουμε, τώρα, τον παρακάτω πίνακα για το ίδιο σχήμα:

παρατηρούμε ότι σχηματίζεται και ένας δεύτερος σταθερός λόγος:

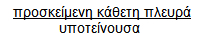
Ο λόγος αυτός ονομάζεται συνημίτονο της γωνίας ω και συμβολίζεται συνω.

Επομένως:

Ο λόγος που σχηματίζεται, αν διαιρέσουμε την προσκείμενη κάθετη πλευρά μίας οξείας γωνίας ω ενός ορθογωνίου τριγώνου με την υποτείνουσα, είναι πάντοτε σταθερός και λέγεται συνημίτονο της γωνίας ω.

Παρατηρήσεις:

α) Γνωρίζουμε ότι σε κάθε ορθογώνιο τρίγωνο η υποτείνουσα είναι μεγαλύτερη από καθεμία από τις κάθετες πλευρές, οπότε οι λόγοι:

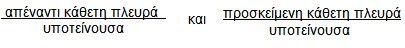
είναι μικρότεροι της μονάδας. Επομένως ισχύουν οι ανισώσεις:

0 < ημω < 1 και 0 < συνω < 1

για οποιαδήποτε οξεία γωνία ω.

β) Αν τώρα διαιρέσουμε το ημω με το συνω θα προκύψει :

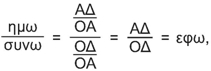
όπως φαίνεται από το ορθογώνιο τρίγωνο ΟΑΔ του σχήματος της προηγούμενης σελίδας. Άρα:

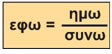
Θεωρούμε ένα ορθογώνιο τρίγωνο ΑΒΓ με κάθετες πλευρές ΑΒ = 15 cm και ΑΓ = 20 cm. Να υπολογίσετε τα ημίτονα και τα συνημίτονα των γωνιών

Τι παρατηρείτε;

Λύση:

2
Να σχεδιαστεί μία οξεία γωνία ω, με $ημω = \dfrac{3}{5}$.

Λύση:

Σύμφωνα με τον ορισμό του ημιτόνου οξείας γωνίας ορθογωνίου τριγώνου, ισχύει:

ημω =.

Επομένως, για να κατασκευάσουμε οξεία γωνία ω με αρκεί να κατασκευάσουμε ένα ορθογώνιο τρίγωνο στο οποίο η μία κάθετη πλευρά του θα είναι ίση με 3 και η υποτείνουσά του ίση με 5.

Για τη γωνία ω ισχύει:

Μικροπείραμα

1.	Στο διπλανό ορθογώνιο τρίγωνο ΑΒΓ είναι:
2.	Στο ορθογώνιο τρίγωνο του διπλανού σχήματος ποιος από τους παρακάτω αριθμούς: Α: συνθ Β: συνφ Γ: ημφ ισούται με ;
3.	Σε ποιο από τα παρακάτω τρίγωνα ισχύει $συνθ = \dfrac{43}{57}$;
4.	Να βάλετε σε κύκλο τη σωστή απάντηση.
5.	Να βάλετε σε κύκλο τις τιμές που δε μπορούν να εκφράζουν το συνημίτονο οξείας γωνίας:
6.	Δίνεται το διπλανό σχήμα. Να χαρακτηρίσετε με Σ (σωστή) ή Λ (λανθασμένη) τις παρακάτω σχέσεις:	Μικροπείραμα
7.	Στο διπλανό σχήμα η γωνία Α είναι ορθή. Να συμπληρώσετε τα κενά στις παρακάτω φάσεις:

1.	Να υπολογίσετε τα ημίτονα και τα συνημίτονα των οξειών γωνιών στα παρακάτω ορθογώνια τρίγωνα.
2.	Δίνεται μια οξεία γωνία ω για την οποία ισχύει $συνω = \dfrac{3}{5}$. Να υπολογίσετε το ημω.
3.	Δίνεται μια οξεία γωνία ω. Να αποδείξετε ότι: α) 2 + 5ημω < 7 β) 4 - 2συνω > 2 γ) 5ημω + 3συνω < 8
4.	Στο διπλανό σχήμα είναι: ΟΑ=10 m, ΟΒ = 12 m και ΟΓ = 8 m. Να υπολογίσετε τις αποστάσεις ΟΔ, ΑΓ και ΒΔ.

O μηχανισμός των Αντικυθήρων ΑΣΤΡΟΛΑΒΟΣ

Αστρολάβος είναι ένα αστρονομικό όργανο που εφευρέθηκε από τον έλληνα αστρονόμο Ίππαρχο το 2ο αιώνα π.Χ. για να μετρήσει το ύψος ενός αστεριού πάνω από τον ορίζοντα, καθώς και τη γωνιακή απόσταση δύο αστεριών.

Στην πρώτη του μορφή ο αστρολάβος ήταν ένας ξύλινος δίσκος, στο κυκλικό πλαίσιο του οποίου ήταν χαραγμένες οι υποδιαιρέσεις του σε μοίρες και μια ακτίνα που έδειχνε το μηδέν (αρχή) των υποδιαιρέσεων.

Στο κέντρο του δίσκου ήταν στερεωμένος ένας κανόνας (χάρακας), που μπορούσε να περιστρέφεται και με τον οποίο γινόταν η στόχευση του αστεριού.

Αργότερα οι αστρολάβοι έγιναν μεταλλικοί, με παραστάσεις από ζωδιακό κύκλο και κάποιους αστρονομικούς χάρτες. Ήταν το κυριότερο όργανο ναυσιπλοΐας κατά το μεσαίωνα και αντικαταστάθηκε από τον εξάντα τον 18ο αιώνα.

Σήμερα οι αστρολάβοι είναι αστρονομικά όργανα μεγίστης ακρίβειας, εφοδιασμένα με διόπτρα μπροστά από την οποία είναι προσαρμοσμένο ένα πρίσμα. Προσδιορίζουν τη χρονική στιγμή κατά την οποία ένα συγκεκριμένο αστέρι βρίσκεται πάνω από τον ορίζοντα σε ορισμένο ύψος, συνήθως 45° ή 60