B1.3: Εμβαδά επίπεδων σχημάτων

1.3.	Εμβαδά επίπεδων σχημάτων

Εμβαδόν τετραγώνου

Ας θεωρήσουμε ένα τετράγωνο πλευράς 5 cm.

Μπορούμε να το χωρίσουμε σε 5 • 5 = 5² = 25 «τετραγωνάκια» πλευράς 1 cm, καθένα από τα οποία έχει εμβαδόν 1 cm². Άρα, το τετράγωνο έχει εμβαδόν 25 cm².

Γενικά:

Το εμβαδόν ενός τετραγώνου πλευράς α ισούται με α².

Εμβαδόν ορθογωνίου

Ας θεωρήσουμε ένα ορθογώνιο με πλευρές 3 cm και 5 cm.

Όπως φαίνεται στο σχήμα, το ορθογώνιο χωρίζεται σε 15 «τετραγωνάκια» εμβαδού 1 cm².

Επομένως, το ορθογώνιο έχει εμβαδόν 3 • 5 = 15 cm².

Γενικά:

Το εμβαδόν ενός ορθογωνίου με πλευρές α, β ισούται με α • β.

Τις πλευρές ενός ορθογωνίου τις λέμε μήκος (τη μεγαλύτερη πλευρά) και πλάτος (τη μικρότερη) και τις ονομάζουμε

διαστάσεις του ορθογωνίου.

Έτσι, μπορούμε να πούμε ότι το γινόμενο των διαστάσεων ενός ορθογωνίου ισούται με το εμβαδόν του ή:

εμβαδόν ορθογωνίου = μήκος • πλάτος.

Μικροπείραμα

Παρατήρηση:

Για να συμβολίσουμε το εμβαδόν κάθε επίπεδου σχήματος, το γράφουμε μέσα σε παρένθεση. Δηλαδή, το εμβαδόν ενός τετραπλεύρου ΑΒΓΔ συμβολίζεται με (ΑΒΓΔ), το εμβαδόν ενός τριγώνου ΖΗΘ συμβολίζεται με (ΖΗΘ) κ.ο.κ.

Μικροπείραμα

Εμβαδόν παραλληλογράμμου

Ας θεωρήσουμε ένα παραλληλόγραμμο ΑΒΓΔ με βάση ΑΒ = β = ΓΔ και ας φέρουμε τα ύψη του ΔΕ = υ και ΓΖ = υ. Μεταφέροντας το τρίγωνο ΑΔΕ στη θέση τού (ίσου με αυτό) τριγώνου ΒΓΖ, παρατηρούμε ότι: το εμβαδόν του παραλληλογράμμου ΑΒΓΔ ισούται με το εμβαδόν του ορθογωνίου ΕΖΓΔ.

Άρα: (ΑΒΓΔ) = (ΕΖΓΔ) = ΕΖ • ΓΖ = β • υ.

Γενικά:

Το εμβαδόν ενός παραλληλογράμμου είναι ίσο με το γινόμενο μίας βάσης του με το αντίστοιχο ύψος.

Μικροπείραμα

Εμβαδόν τυχαίου τριγώνου

Ας θεωρήσουμε ένα τυχαίο τρίγωνο ΑΒΓ που δεν είναι ορθογώνιο και ας πάρουμε και άλλο ένα τρίγωνο ίδιο με αυτό.

Αν τοποθετήσουμε το δεύτερο τρίγωνο δίπλα στο πρώτο, όπως φαίνεται στα διπλανά σχήματα, τότε θα σχηματιστεί ένα παραλληλόγραμμο ΑΒΓΔ, που θα έχει ως βάση β, τη βάση ΒΓ του ΑΒΓ και ως ύψος υ, το ύψος του ΑΒΓ, από την κορυφή Α.

Είτε το τρίγωνο ΑΒΓ είναι οξυγώνιο, είτε είναι αμβλυγώνιο, το εμβαδόν του θα είναι ίσο με το μισό του παραλληλογράμμου ΑΒΓΔ που σχηματίζεται, αν τοποθετήσουμε άλλο ένα τρίγωνο ίσο με το ΑΒΓ, όπως φαίνεται στα διπλανά σχήματα.

Επομένως, θα ισχύει:

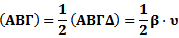
όπου β η βάση του ΑΒΓ και υ το αντίστοιχο ύψος.

Γενικά:

Το εμβαδόν ενός τριγώνου είναι ίσο με το μισό του γινομένου μιας βάσης του με το αντίστοιχο ύψος.

Μικροπείραμα

Εμβαδόν ορθογωνίου τριγώνου

Όταν το τρίγωνο ΑΒΓ είναι ορθογώνιο, τότε η μία από τις κάθετες πλευρές είναι η βάση β και η άλλη το ύψος του.

Επομένως:

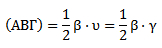
Το εμβαδόν ενός ορθογωνίου τριγώνου είναι ίσο με το μισό του γινομένου των δύο κάθετων πλευρών του.

Εμβαδόν τραπεζίου

Ας θεωρήσουμε το τραπέζιο ΑΓΔΕ που έχει μεγάλη βάση ΑΓ = Β, μικρή βάση ΕΔ = β και ύψος ΕΘ = υ.

Θεωρώντας άλλο ένα ίσο τραπέζιο με το ΑΓΔΕ σχηματίζουμε ένα παραλληλόγραμμο ΑΖΗΕ, όπως φαίνεται στο

διπλανό σχήμα.

Το παραλληλόγραμμο που σχηματίσαμε έχει βάση (β + Β) και ύψος υ.

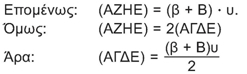
Το εμβαδόν ενός τραπεζίου είναι ίσο με το γινόμενο του ημιαθροίσματος των βάσεών του με το ύψος του.

Μικροπείραμα Μικροπείραμα

Να συμπληρώσετε τον διπλανό πίνακα:

Μήκος ορθογωνίου	Πλάτος ορθογωνίου	Περίμετρος ορθογωνίου	Εμβαδόν ορθογωνίου
12 m	10 m
17 m		44m
	9 m		45 m²
33 m			330 m²

Λύση:

Με τη βοήθεια της σχέσης: εμβαδόν ορθογωνίου = μήκος • πλάτος, συμπληρώνουμε τον πίνακα:

Μήκος ορθογωνίου	Πλάτος ορθογωνίου	Περίμετρος ορθογωνίου	Εμβαδόν ορθογωνίου
12 m	10 m	44 m	120 m²
17 m	5 m	44 m	85 m²
5 m	9 m	28 m	45 m²
33 m	10 m	86 m	330 m²

H αίθουσα Φυσικής στο σχολείο της Άννας αποφασίστηκε να στρωθεί με τετράγωνα πλακάκια που το καθένα έχει πλευρά 25 cm.

α) Να βρείτε πόσα πλακάκια θα χρειαστούν, αν το δάπεδο της τάξης έχει διαστάσεις 12 m μήκος και 8 m πλάτος.

β) Αν κάθε πλακάκι κοστίζει 0,5 €, πόσα χρήματα θα χρειαστούν για να στρωθεί η τάξη;

Λύση:

α) Το εμβαδόν του δαπέδου είναι: Ε_ΔΑΠ = 12 • 8 = 96 (m²) και το εμβαδόν σε κάθε πλακάκι είναι:

Ε_ΠΛΑΚ = 25 • 25 = 625 (cm²) = 0,0625 (m²).

Διαιρώντας τα δύο αυτά εμβαδά βρίσκουμε πόσα πλακάκια χρειάζονται για να στρωθεί η τάξη:

β) Αφού χρειάζονται 1536 πλακάκια και το κάθε πλακάκι κοστίζει 0,5 €, το συνολικό κόστος θα είναι: 1536 • 0,5 = 768 €.

Μικροπείραμα

Στο σχολείο της Κάτιας το μαθητικό συμβούλιο εκδίδει μια εφημερίδα που κάθε φύλλο της έχει διαστάσεις 42 cm μήκος και 30 cm πλάτος.

Να υπολογίσετε τη συνολική επιφάνεια του χαρτιού που θα χρησιμοποιηθεί, για να τυπωθούν 800 αντίτυπα της εφημερίδας, αν κάθε αντίτυπο έχει 8 φύλλα.

Λύση:

Το εμβαδόν κάθε φύλλου είναι 30 • 42 = 1260 (cm²).

Aφού κάθε αντίτυπο έχει 8 φύλλα, χρειάζονται 8 • 1260 = 10080 (cm²) χαρτί για κάθε αντίτυπο.

Eπομένως, για να τυπωθούν 800 αντίτυπα, θα χρειαστούν: 800 • 10080 = 8064000 (cm²) = 806,4 (m²) χαρτί.

Στο τρίγωνο ΑΒΓ του σχήματος φέρνουμε τη διάμεσο ΑΜ.

Να αποδείξετε ότι τα τρίγωνα ΜΑΒ και ΜΑΓ έχουν το ίδιο εμβαδόν.

Λύση:

Φέρνουμε το ύψος ΑΗ.

Τότε το τρίγωνο ΜΑΒ έχει εμβαδόν:

Το τρίγωνο ΜΑΓ έχει εμβαδόν: .

Όμως, ΜΒ = ΜΓ, επειδή το Μ είναι το μέσο της ΒΓ (η ΑΜ είναι διάμεσος).

Άρα: (ΜΑΒ) = (ΜΑΓ).

Ένα οικόπεδο, όπως φαίνεται στο παρακάτω σχήμα, πωλείται προς 300 € το m².

Ποια είναι η αξία του οικοπέδου;

Λύση:

Βρίσκουμε πρώτα το εμβαδόν του οικοπέδου.

Αυτό αποτελείται από το ορθογώνιο ΑΒΓΔ και το τραπέζιο ΒΕΖΓ.

Το εμβαδόν του ορθογωνίου είναι: (ΑΒΓΔ) = 18 • 15 = 270 (m²).

To εμβαδόν του τραπεζίου είναι:

Άρα, το εμβαδόν του οικοπέδου είναι 270 + 115 = 385 (m²).

Για να βρούμε την αξία πώλησης του οικοπέδου, πολλαπλασιάζουμε το εμβαδόν του με την τιμή πώλησης του τετραγωνικού μέτρου.

Άρα, η αξία του οικοπέδου είναι: 385 • 300 = 115.500 €.

Στο παρακάτω σχήμα:

α) Να εκφράσετε το εμβαδόν του τραπεζίου ΑΒΓΔ ως συνάρτηση του x.

β) Αν το εμβαδόν του τραπεζίου ΑΒΓΔ είναι το τριπλάσιο από το εμβαδόν του ορθογωνίου ΑΕΖΔ, να υπολογίσετε το x.

Λύση:

α) Στο τραπέζιο ΑΒΓΔ, η μικρή βάση είναι ΔΓ = x + 3 (cm), η μεγάλη βάση είναι ΑΒ= x + 1 + 3 = x + 4 (cm) και το ύψος του είναι ΔΑ = 6 (cm).

Άρα, το εμβαδόν του είναι:

β) Το εμβαδόν του ορθογωνίου είναι (ΑΕΖΔ) = 3 • 6 = 18 (cm²).

Αφού το εμβαδόν του τραπεζίου είναι τριπλάσιο από το εμβαδόν του ορθογωνίου, έχουμε:

(ΑΒΓΔ) = 3 • (ΑΕΖΔ) ή 3(2x + 7) = 3 • 18 Δηλαδή: 2x + 7 = 18 ή 2x = 11 ή x = 5,5 (cm).

1.	Στο διπλανό σχήμα:

		Α	Β	Γ
1	To εμβαδόν του ΑΒΗΘ είναι:	3	6	9
2	To εμβαδόν του ΑΓΖΘ είναι:	6	12	18
3	To εμβαδόν του ΑΓΕΗ είναι:	12	18	21
4	To εμβαδόν του ΑΗΓ είναι:	9	12	4,5
5	To εμβαδόν του ΒΖΗ είναι:	9	12	4,5
6	To εμβαδόν του ΑΔΖΗ είναι:	12	18	21
7	To εμβαδόν του ΑΔΕΗ είναι:	22,5	18	27
8	To εμβαδόν του ΑΒΕΘ είναι:	22,5	18	21

Nα επιλέξετε τη σωστή απάντηση.

2.	Στο διπλανό σχήμα:

		Α	Β	Γ
1	To εμβαδόν του παραλληλογράμμου ΑΒΓΔ είναι:	24	9	18
2	To ύψος x που αντιστοιχεί στην πλευρά ΑΔ είναι:	5,5	9	4,5
3	To εμβαδόν του παραλληλογράμμου ΕΖΗΘ είναι:	24	12	32
4	Η πλευρά x = ΕΘ είναι:	4	6	5
5	Ποιο από τα επόμενα δεν είναι ίσο με το εμβαδόν του τριγώνου ΑΒΓ;
6	Το εμβαδόν του τριγώνου ΕΘΗ είναι:	32	16	20
7	Το ύψος ΘΚ που αντιστοιχεί στην πλευρά ΕΗ είναι:	4	5	6
8	Το διπλανό παραλληλόγραμμο ΑΒΓΔ έχει εμβαδόν 16cm² και το Ε είναι το μέσο της πλευράς ΓΔ. Το εμβαδόν του τριγώνου ΚΕΓ είναι:	4	6	8
9	Το εμβαδόν του μπλε παραλληλογράμμου είναι:	5	4	8
10	Το εμβαδόν κάθε πράσινου τριγώνου είναι:	16	20	17,5
11	Αν το εμβαδόν του παραλληλογράμμου ΑΒΕΔ είναι 12cm² και το Ε είναι το μέσο της πλευράς ΓΔ, τότε το εμβαδόν του τραπεζίου ΑΒΓΔ είναι:	24	16	18

1.	Αν η περίμετρος ενός τετραγώνου είναι 60 cm, να υπολογίσετε το εμβαδόν του.
2.	Οι διαστάσεις ενός φύλλου στο εικοσάφυλλο τετράδιο του Σταύρου είναι 21 cm και 30 cm. Να υπολογίσετε πόση επιφάνεια χαρτιού έχει όλο το τετράδιο.
3.	Στο παρακάτω σχήμα να αποδείξετε ότι τα εμβαδά του ροζ και του κίτρινου σχήματος είναι ίσα. Μικροπείραμα
4.	Να κατασκευάσετε ένα τετράγωνο ΑΒΓΔ. Στη συνέχεια να προεκτείνετε την πλευρά ΑΒ του τετραγώνου και να πάρετε τμήμα ΒΕ = ΑΒ. α) Να αποδείξετε ότι το τετράγωνο ΑΒΓΔ και το τρίγωνο ΑΕΔ έχουν ίσα εμβαδά. β) Να αποδείξετε ότι το εμβαδόν του ΑΕΔ είναι διπλάσιο από το εμβαδόν του ΒΓΕ.
5.	Να υπολογίσετε τα εμβαδά των δύο σχημάτων στο παρακάτω σχήμα, αν x = 5 cm. Στη συνέχεια, να εξηγήσετε γιατί αυτά είναι ίσα για οποιαδήποτε τιμή του x.
6.	Ένα τετράγωνο και ένα τραπέζιο έχουν ίσα εμβαδά. Αν οι βάσεις του τραπεζίου είναι 12 cm και 20 cm και το ύψος του είναι 4 cm, να υπολογίσετε το εμβαδόν του τετραγώνου.
7.	Ένας ορθογώνιος κήπος έχει διαστάσεις 40 m και 25 m. Τον κήπο διασχίζουν δύο κάθετα μεταξύ τους δρομάκια. Το ένα παράλληλο προς τη μεγάλη πλευρά του κήπου με πλάτος 0,6 m και το άλλο με πλάτος 0,8 m. Το υπόλοιπο τμήμα θα φυτευτεί με γκαζόν. Να υπολογίσετε το κόστος της κατασκευής του γκαζόν, αν ο γεωπόνος χρεώνει 12 € κάθε m² γκαζόν.
8.	Τα παρακάτω ορθογώνια έχουν τις ίδιες διαστάσεις. Εξηγήστε γιατί τα πράσινα μέρη των δύο ορθογωνίων έχουν ίσα εμβαδά.
9.	Στο παρακάτω σχήμα φαίνεται οικόπεδο σχήματος ορθογωνίου, το οποίο διασχίζει διαγώνια ένας δρόμος σταθερού πλάτους. α) Να αποδείξετε ότι τα τριγωνικά οικόπεδα που απομένουν έχουν ίσα εμβαδά. β) Να υπολογίσετε το x, ώστε ο δρόμος να «αποκόπτει» από το οικόπεδο τμήμα του οποίου το εμβαδόν να είναι ίσο με του εμβαδού που απομένει στο οικόπεδο.
10.	Στο τετράγωνο ΑΒΓΔ του παρακάτω σχήματος είναι Μ και Ν τα μέσα των πλευρών του ΑΔ και ΔΓ αντίστοιχα. α) Να αποδείξετε ότι τα τρίγωνα ΜΑΒ και ΝΓΒ έχουν ίσα εμβαδά. β) Να αποδείξετε ότι το τετράπλευρο ΒΜΔΝ έχει εμβαδόν όσο είναι το άθροισμα των εμβαδών των παραπάνω τριγώνων. Μικροπείραμα
11.	Στα παρακάτω σχήματα κάθε τετραγωνάκι έχει πλευρά 1 cm. Να βρείτε τα εμβαδά των 12 σχημάτων που δίνονται:

12.	Στο τετράπλευρο του διπλανού σχήματος οι διαγώνιες είναι κάθετες. Αν ΒΔ=5 CM, ΟΑ=3CM και ΟΓ=6cm, να υπολογίσετε το εμβαδόν του τετράπλευρου.
13.	Να υπολογίσετε το x σε καθένα από τα παρακάτω σχήματα.
14.	Να υπολογίσετε τα εμβαδά των παρακάτω σχημάτων:
15.	Να βρείτε το εμβαδόν του πορτοκαλί τετραγώνου του παρακάτω σχήματος. Μικροπείραμα
16.	Στο παρακάτω σχήμα δίνεται η κάτοψη ενός διαμερίσματος.

	Να βρείτε: α) Το εμβαδόν κάθε δωματίου. β) Το εμβαδόν του γωνιακού διαδρόμου. γ) Το εμβαδόν της βεράντας.
17.	Στο παρακάτω σχήμα φαίνεται το τοπογραφικό διάγραμμα ενός κτήματος το οποίο πωλείται προς 20.000 € το στρέμμα. α) Να βρεθεί η αξία του κτήματος. β) Πόσα κλήματα μπορούμε να φυτέψουμε στο κτήμα αυτό, αν κάθε κλήμα απαιτεί 2,5 m² χώρο;

Πίσω από την κουρτίνα κρύβονται ένα τετράγωνο, ένα ορθογώνιο και ένα ορθογώνιο τρίγωνο.

Βρείτε τη θέση και το εμβαδόν καθενός, αν γνωρίζετε ότι:

Το ορθογώνιο έχει τετραπλάσιο εμβαδόν και βρίσκεται πιο αριστερά από το τετράγωνο.
Ένα σχήμα εμβαδού 100 cm² βρίσκεται δεξιά από το ορθογώνιο τρίγωνο.
Δεξιά από ένα σχήμα με τέσσερις ορθές γωνίες βρίσκεται το ορθογώνιο τρίγωνο.
Οι κάθετες πλευρές του ορθογωνίου τριγώνου είναι ίσες με τις κάθετες πλευρές του ορθογωνίου.