| 1 |
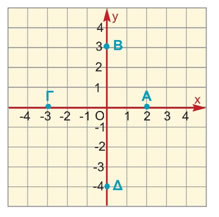
Να βρείτε τις συντεταγμένες των σημείων Α, Β, Γ και Δ του παρακάτω σχήματος. Τι συμπεραίνετε; |
Λύση: |
Παρατηρούμε ότι από τα σημεία Α και Γ οι κάθετες προς τον άξονα y'y αντιστοιχούν στο σημείο Ο,
οπότε αυτά τα σημεία έχουν τεταγμένες 0. Άρα είναι Α(2, 0), Γ(-3, 0).
Ομοίως, από τα σημεία Β και Δ οι κάθετες προς τον άξονα x'x αντιστοιχούν στο σημείο Ο,
οπότε τα σημεία αυτά έχουν τετμημένη 0. Άρα είναι Β(0, 3) και Δ(0, -4).
Δηλαδή:
Κάθε σημείο του άξονα x'x έχει τεταγμένη 0
και
κάθε σημείο του άξονα y 'y έχει τετμημένη 0. |
|
| 2 |
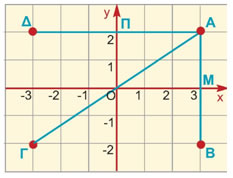
Δίνεται το σημείο Α(3, 2). Να βρείτε το συμμετρικό του Α ως προς:
α) τον άξονα x'x
β) τον άξονα y'y
γ) την αρχή Ο των αξόνων.
Ποιες είναι οι συντεταγμένες των σημείων αυτών; |
Λύση: |
Από το Α φέρνουμε κάθετες ΑΜ και ΑΠ στους άξονες x'x και y'y.
α) Προεκτείνουμε την ΑΜ κατά τμήμα ΜΒ = ΜΑ.
Το σημείο Β είναι το συμμετρικό του Α ως προς τον άξονα x'x και έχει συντεταγμένες (3, -2).
β) Προεκτείνουμε την ΑΠ κατά τμήμα ΠΔ = ΠΑ.
Το σημείο Δ είναι το συμμετρικό του Α ως προς τον άξονα y'y και έχει συντεταγμένες (-3, 2).
γ) Ενώνουμε το Α με την αρχή Ο των αξόνων και προεκτείνουμε κατά τμήμα ΟΓ = ΟΑ.
Το σημείο Γ είναι το συμμετρικό του Α ως προς την αρχή Ο και έχει συντεταγμένες (-3, -2) |
|
Μικροπείραμα  Μικροπείραμα Μικροπείραμα 
| 3 |
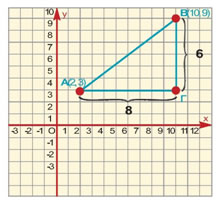
Δίνονται τα σημεία Α(2, 3) και Β(10, 9). Να υπολογίσετε την απόστασή τους ΑΒ.
Τι συμπεραίνετε; |
Λύση: |
Σχηματίζουμε το ορθογώνιο τρίγωνο ΑΒΓ του διπλανού σχήματος.
Τότε το σημείο Γ έχει συντεταγμένες (10, 3),
οπότε ΑΓ = 10 - 2 = 8 και ΒΓ = 9 - 3 = 6.
Από το Πυθαγόρειο θεώρημα έχουμε ότι:
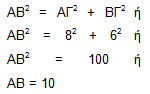
Γενικότερα:
Αν δίνονται δύο σημεία , |
|
η απόστασή τους υπολογίζεται από τον τύπο: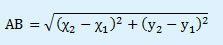 |
Μικροπείραμα  |
|
| 4 |
Έχει διαπιστωθεί ότι το νερό της θάλασσας δεν έχει παντού την ίδια θερμοκρασία.
Όσο πιο βαθιά κατεβαίνουμε, τόσο πιο κρύο γίνεται το νερό.
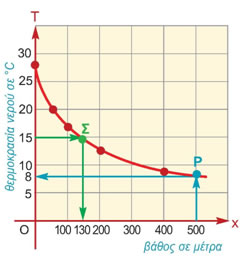
Ένα ωκεανογραφικό σκάφος κάνει μετρήσεις θερμοκρασίας σε διάφορα βάθη στο βόρειο Αιγαίο, με τα εξής αποτελέσματα :

όπου Τ είναι η θερμοκρασία (σε βαθμούς Κελσίου) η οποία μεταβάλλεται ως συνάρτηση του βάθους x (σε μέτρα).
α) Να κάνετε τη γραφική παράσταση της συνάρτησης αυτής.
β)Να χρησιμοποιήσετε τη γραφική παράσταση για να εκτιμήσετε τη θερμοκρασία του νερού σε βάθος 500 μέτρων.
γ) Σε ποιο βάθος από την επιφάνεια της θάλασσας η θερμοκρασία είναι 15°C; |
Λύση: |
α) Σ' ένα σύστημα αξόνων τοποθετούμε τα σημεία με συντεταγμένες
(0, 28), (50, 20), (100, 17), (200, 12) και (400, 9). Χρησιμοποιούμε ένα μη ορθοκανονικό σύστημα αξόνων. Στον άξονα x'x η μονάδα μέτρησης αντιστοιχεί σε 100 μέτρα, ενώ στον άξονα y'y η μονάδα μέτρησης αντιστοιχεί σε θερμοκρασία 5°C.
Στη συνέχεια, ενώνουμε με μία καμπύλη τα σημεία αυτά.
β) Για να βρούμε τη θερμοκρασία του νερού σε βάθος 500 μέτρων, από το σημείο με τετμημένη 500 του άξονα x'x φέρνουμε ευθεία παράλληλη στον άξονα y'y, που τέμνει την γραφική παράσταση στο σημείο Ρ. Στη συνέχεια, από το Ρ φέρνουμε παράλληλη προς τον άξονα x'x, που τέμνει τον άξονα y'y στο σημείο με τεταγμένη (περίπου) 8.
Άρα, η θερμοκρασία σε βάθος x = 500 m είναι (περίπου) T = 8°C.
γ) Για να βρούμε σε ποιο βάθος η θερμοκρασία είναι 15°C, φέρνουμε από το σημείο με τεταγμένη 15 του άξονα y'y παράλληλη προς τον άξονα x'x που τέμνει τη γραφική παράσταση στο σημείο Σ. Στη συνέχεια, από το Σ φέρνουμε παράλληλη προς τον άξονα y'y, που τέμνει τον άξονα x'x στο σημείο με τετμημένη (περίπου) 130 m.
Άρα, η θερμοκρασία είναι 15°C σε βάθος (περίπου) x = 130 m.
Μικροπείραμα  |
 |
| 5 |
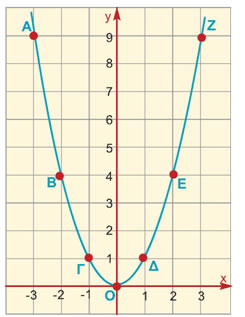
Να σχεδιάσετε τη γραφική παράσταση της συνάρτησης 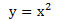 |
Λύση: |
Σχηματίζουμε, καταρχάς, έναν πίνακα τιμών της συνάρτησης.

Στη συνέχεια, τοποθετούμε σ' ένα σύστημα αξόνων
τα σημεία με συντεταγμένες (x, y) του παραπάνω πίνακα.
Έτσι, βρίσκουμε τα σημεία Α(-3, 9), Β(-2, 4), Γ(-1, 1), Ο(0, 0),
Δ(1, 1), Ε(2, 4) και Ζ(3, 9).
Στη συνέχεια, ενώνουμε με τη σειρά τα σημεία αυτά.
Η καμπύλη που προκύπτει είναι η γραφική παράσταση της συνάρτησης
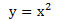
|
|
| |
1. |
Να αντιστοιχίσετε σε κάθε σημείο τις συντεταγμένες του:
| Σημείο |
Συντεταγμένες |
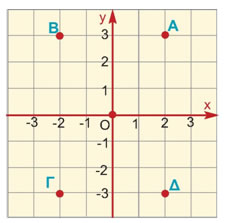 |
| Α |
(2, 3) (3, 2) |
| Β |
(-2, 3) (-3, 2) |
| Γ |
(-2, -3) (-3, -2) |
| Δ |
(2, -3) (3, -2) |
|
2. |
Να συμπληρώσετε τον πίνακα, όπως φαίνεται στο παράδειγμα της 1ης γραμμής.
| Σημείο Α |
Συμμετρικό του Α ως προς τον x'x
|
Συμμετρικό του Α ως προς τον y'y
|
Συμμετρικό του Α ως προς το O
|
(-2, 3)
|
(-2, -3)
|
(2, 3)
|
(2, -3)
|
(3, 5)
|
|
|
|
(-3, 5)
|
|
|
|
(-3, -5)
|
|
|
|
(3, -5)
|
|
|
|
|
3. |
Στο διπλανό σχήμα είναι:
α) ΑΒ < ΑΓ,
β) ΑΒ > ΑΓ,
γ) ΑΒ = ΑΓ
Να επιλέξετε τη σωστή απάντηση. |
|
4. |
Στο διπλανό σχήμα είναι:
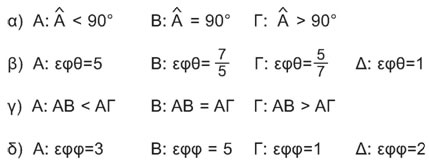
Να επιλέξετε τη σωστή απάντηση. |
 |
5. |
Στο διπλανό σχήμα δίνεται η γραφική παράσταση μιας συνάρτησης
α) για x=1, είναι y =........ Α: -1 Β: 2 Γ: 3 Δ: 5
β) για x=3, είναι y =........ Α: -1 Β: 2 Γ: 3 Δ: 5
γ) για y=6, είναι x =........ Α: -1 Β: 2 Γ: 3 Δ: 5
δ) για y=2, είναι x =....... Α: -1 Β: 2 Γ: 3 Δ: 5
Να επιλέξετε τη σωστή απάντηση. |
|
|
| |
1. |
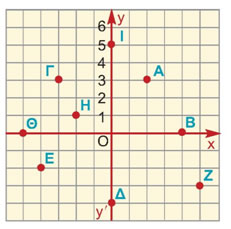
Στο παρακάτω σχήμα να βρείτε τις συντεταγμένες των σημείων
Α, Β, Γ, Δ, Ε, Ζ, Η, Θ και Ι.
Μικροπείραμα  |
2. |
Σ' ένα τετραγωνισμένο χαρτί να σχεδιάσετε ένα σύστημα αξόνων και να σημειώσετε τα σημεία :

|
3. |
Δίνονται τα σημεία :
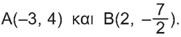
Σε τετραγωνισμένο χαρτί να βρείτε τις συντεταγμένες των συμμετρικών
τους σημείων ως προς τον άξονα x'x, τον άξονα y'y και την
αρχή Ο των αξόνων. |
4. |
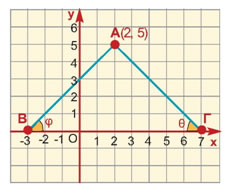
α) Στο παρακάτω σχήμα να βρείτε τις συντεταγμένες
των σημείων Α, Β και Γ.
β) Να επιλέξετε τη σωστή απάντηση.
i) To μήκος ΒΓ ισούται με:
Α: 1 + 3 = 4
Β: 2 - 2 = 0
Γ: 3 - 1 = 2
Δ: -1 - 3 = -4
ii) Το μήκος ΑΓ ισούται με:
Α: 3 - 3 = 0
Β: 1 + 2 = 3
Γ: 1 - 2 = -1
Δ: 2 - 1 = 1
γ) Αφού παρατηρήσετε ότι το τρίγωνο ΑΒΓ είναι ορθογώνιο στο Γ,
να επαληθεύσετε με τη βοήθεια του Πυθαγόρειου θεωρήματος
ότι η απόσταση ΑΒ είναι ίση με 5.
|
5. |
Να βρείτε τις αποστάσεις των παρακάτω σημείων από τους άξονες x'x και y'y.
α) Α(3, 5)
β) B(-3, 2)
γ) Γ(0, -4) |
|
|
6 . |
Να βρείτε τις αποστάσεις των σημείων:
α) Α(3, 5) και Β(5, 1) β) Α(-2, 1) και Β(2, -3)
γ) Α(3,-5) και Β(-2,-5) δ) Α(-5,-7) και Β(-5,2) |
7. |
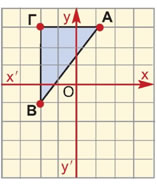
Ένα πλοίο Π κινείται με ταχύτητα 8 μίλια την ώρα και κατευθύνεται προς το λιμάνι Λ.
Η θέση του πλοίου ως προς ένα σύστημα συντεταγμένων
με αρχή το Λ και μονάδα μέτρησης το 1 μίλι, είναι (-8, 15).
Σε πόση ώρα θα φτάσει στο λιμάνι;
|
8. |
Η πίεση P (σε cm Hg) του αέρα ως συνάρτηση του ύψους h
από το έδαφος φαίνεται στον παρακάτω πίνακα.

α) Να κατασκευάσετε σε ορθογώνιο σύστημα συντεταγμένων τη γραφική παράσταση της συνάρτησης αυτής.
β) Ποια είναι η πίεση σε ύψος 1,5 km από το έδαφος;
γ) Σε ποιο ύψος η πίεση είναι περίπου ίση με 70 cm Hg; |
9. |
H θερμοκρασία Τ του αέρα ως συνάρτηση του ύψους h φαίνεται
στον παρακάτω πίνακα.

α) Να κατασκευάσετε σε ορθογώνιο σύστημα συντεταγμένων τη γραφική παράσταση της συνάρτησης αυτής.
β) Πόση περίπου είναι η θερμοκρασία του αέρα σε ύψος 500 μέτρων;
γ) Σε ποιο ύψος η θερμοκρασία του αέρα είναι περίπου 12°C;
Μικροπείραμα  |
10. |
Όταν ένα σώμα (π.χ. μια μπάλα) πέφτει από ένα ψηλό σημείο (π.χ. από τον τελευταίο όροφο ενός ουρανοξύστη ύψους 100 m) δεν κινείται ομαλά (με σταθερή ταχύτητα), αλλά εκτελεί επιταχυνόμενη κίνηση.
Στον παρακάτω πίνακα φαίνεται η απόσταση x που διανύει το σώμα ως συνάρτηση του χρόνου t.
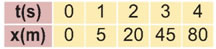
Να κατασκευάσετε σε ορθογώνιο σύστημα τη γραφική παράσταση της συνάρτησης αυτής. |
|
|