Άρρητοι αριθμοί
Οι Πυθαγόρειοι πίστευαν ότι ο λόγος δύο οποιωνδήποτε μεγεθών μπορεί να εκφραστεί ως λόγος δύο φυσικών αριθμών. Στην πεποίθηση αυτή είχαν στηρίξει όλη την κοσμοθεωρία τους και προσπαθούσαν να επιλύσουν προβλήματα από τον πραγματικό κόσμο.
Η πρώτη κρίση στα Μαθηματικά εμφανίστηκε όταν, σύμφωνα με την παράδοση, ο Ίππασος ο Μεταπόντιος (450 π.Χ. περίπου) «αποκάλυψε» τον «άρρητο» 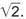
Σύντομα βρέθηκαν και άλλοι άρρητοι αριθμοί. Ο Εύδοξος ο Κνίδιος (407 - 354 π.Χ.) ήταν αυτός που έβγαλε τους Πυθαγόρειους από την κρίση θεμελιώνοντας ένα μεγάλο μέρος της μελέτης των άρρητων αριθμών. Ας δούμε, όμως, πώς οδηγηθήκαμε στην ύπαρξη των αρρήτων. Στο διπλανό σχήμα έχουμε ένα τετράγωνο πλευράς 1cm και θέλουμε να υπολογίσουμε τη διαγώνιο x του τετραγώνου.
Από το Πυθαγόρειο θεώρημα έχουμε: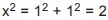 , οπότεx = $\sqrt{2}$. , οπότεx = $\sqrt{2}$.
Oι Πυθαγόρειοι απέδειξαν ότι o αριθμός $\sqrt{2}$ δεν μπορεί ναπάρει τη μορφή $\dfrac{μ}{ν}$, όπου μ, ν ακέραιοι με ν ≠ 0, δηλαδή δενείναι ρητός. Γι’ αυτό λέγεται άρρητος.
Γενικά :
| Kάθε αριθμός που δεν μπορεί να πάρει τη μορφή $\dfrac{μ}{ν}$, όπου μ, νακέραιοι με ν ≠ 0, ονομάζεται άρρητος αριθμός. |
Μικροπείραμα 
Για να προσεγγίσουμε τον αριθμό x, παρατηρούμε διαδοχικά ότι:
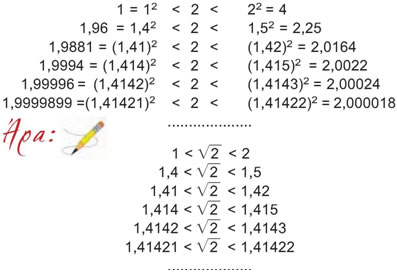
Στην προηγούμενη παράγραφο συμβολίζαμε με 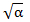 τον θετικό αριθμό που, όταν υψωθεί στο τετράγωνο, μας δίνει τον αριθμό α. τον θετικό αριθμό που, όταν υψωθεί στο τετράγωνο, μας δίνει τον αριθμό α.
Επομένως, τον αριθμό x που προσπαθούμε να βρούμε έτσι ώστε 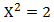 , μπορούμε να τον συμβολίζουμε με , μπορούμε να τον συμβολίζουμε με 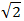 , αλλά δεν μπορούμε να τον υπολογίσουμε με ακρίβεια, παρά μόνο προσεγγιστικά. Αφού είναι άρρητος, δε μπορεί να γραφεί ως ρητός ή δεκαδικός με γνωστά ψηφία. , αλλά δεν μπορούμε να τον υπολογίσουμε με ακρίβεια, παρά μόνο προσεγγιστικά. Αφού είναι άρρητος, δε μπορεί να γραφεί ως ρητός ή δεκαδικός με γνωστά ψηφία.
Με τους προηγούμενους υπολογισμούς μπορούμε μόνο να προσεγγίσουμε τον 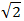 ως εξής: ως εξής:
Αποδεικνύεται, επίσης, ότι και οι αριθμοί 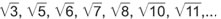 είναι άρρητοι. Αργότερα, θα μάθουμε ότι υπάρχουν και άλλοι άρρητοι που δεν είναι ρίζες ρητών αριθμών, όπως ο γνωστός από τη μέτρηση του κύκλου αριθμός π. είναι άρρητοι. Αργότερα, θα μάθουμε ότι υπάρχουν και άλλοι άρρητοι που δεν είναι ρίζες ρητών αριθμών, όπως ο γνωστός από τη μέτρηση του κύκλου αριθμός π.
Μικροπείραμα 
Σχόλιο:
Τις τετραγωνικές ρίζες μπορούμε να τις προσεγγίσουμε με τη βοήθεια ενός μικροϋπολογιστή τσέπης ως εξής:
Για να προσεγγίσουμε τον αριθμό 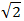 , πατάμε διαδοχικά τα πλήκτρα , πατάμε διαδοχικά τα πλήκτρα  και και  οπότε στην οθόνη βλέπουμε τον αριθμό 1,414213 που είναι μια προσέγγιση του οπότε στην οθόνη βλέπουμε τον αριθμό 1,414213 που είναι μια προσέγγιση του 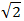 , με έξι δεκαδικά ψηφία. , με έξι δεκαδικά ψηφία.
Παλαιότερα, για τον υπολογισμό των ριζών χρησιμοποιούσαμε ειδικούς πίνακες.
Πραγματικοί αριθμοί
Ας μελετήσουμε όλα τα σύνολα αριθμών που έχουμε συναντήσει.
 Οι φυσικοί αριθμοί: 0, 1, 2, 3, ... παριστάνονται στη διπλανή ευθεία με σημεία. Οι φυσικοί αριθμοί: 0, 1, 2, 3, ... παριστάνονται στη διπλανή ευθεία με σημεία.
Στην αρχή Ο έχουμε τοποθετήσει το μηδέν (0).
 Οι ακέραιοι αριθμοί: ... -3, -2, -1, 0, 1, 2, 3 ... παριστάνονται πάλι με σημεία. Οι ακέραιοι αριθμοί: ... -3, -2, -1, 0, 1, 2, 3 ... παριστάνονται πάλι με σημεία.
Τοποθετούμε στα δεξιά της αρχής Ο τους θετικούς ακέραιους αριθμούς και στα αριστερά τους αρνητικούς.
 Το σύνολο των ρητών αριθμών, δηλαδή των αριθμών που μπορούν να γραφούν στη μορφή Το σύνολο των ρητών αριθμών, δηλαδή των αριθμών που μπορούν να γραφούν στη μορφή 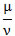 , ,
όπου μ ακέραιος και ν φυσικός αριθμός . Οι ρητοί αριθμοί έχουν γνωστή δεκαδική μορφή και γεμίζουν την
ευθεία, αλλά όχι πλήρως.
 Οι πραγματικοί αριθμοί αποτελούνται όχι μόνο από τους ρητούς αλλά και όλους τους άρρητους. Οι πραγματικοί αριθμοί αποτελούνται όχι μόνο από τους ρητούς αλλά και όλους τους άρρητους.
Οι πραγματικοί αριθμοί καλύπτουν πλήρως την ευθεία, δηλαδή κάθε σημείο της ευθείας αντιστοιχεί σε έναν πραγματικό αριθμό και αντίστροφα κάθε πραγματικός αριθμός αντιστοιχεί σε μοναδικό σημείο της ευθείας.
Για το λόγο αυτό, την ευθεία αυτή την ονομάζουμε ευθεία ή άξονα των πραγματικών αριθμών.
|