Ανισώσεις
Όπως γνωρίζουμε, η σχέση που συνδέει τα βάρη μιας ζυγαριάς που δεν ισορροπεί, είναι μία σχέση ανισότητας.
Για παράδειγμα, για τα βάρη α και β του διπλανού σχήματος έχουμε την ανισότητα:
α < β ή ισοδύναμα, την ανισότητα β > α.
Μερικές φορές, επίσης, χρησιμοποιούμε το σύμβολο «≤» ή το σύμβολο «≥».
Γράφουμε: α ≤ β, όταν είναι α = β ή α < β και διαβάζουμε: «το α είναι μικρότερο ή ίσο του β».
Παρατήρηση:
Αν ένας αριθμός α είναι μικρότερος από τον αριθμό β, τότε ο α βρίσκεται «πιο αριστερά» από τον β στην
ευθεία των αριθμών. Η ίδια ανίσωση βέβαια μπορεί να γραφεί και β > α, γιατί ο β βρίσκεται «πιο δεξιά»
από τον α.
| 1 |
Δίνονται οι αριθμοί α και β του παρακάτω σχήματος. Να συμπληρώσετε ένα από τα σύμβολα «<», «>», «=» στη θέση των κενών.
α) α........β β) α + 2........β + 2
γ) α + 12.....β + 12 δ) α – 7........β – 7 |
Λύση
α) Ο α βρίσκεται «πιο αριστερά» από τον β στην ευθεία των αριθμών, οπότε α < β.
β) Ο α + 2 βρίσκεται «πιο αριστερά» από τον β + 2, οπότε α + 2 < β + 2.
γ) Ο α + 12 βρίσκεται «πιο αριστερά» από τον β + 12, οπότε α + 12 < β + 12
δ) Ο α – 7 βρίσκεται «πιο αριστερά» από τον β – 7, οπότε α – 7 < β – 7.
Γενικά, για την πρόσθεση και την αφαίρεση, ισχύει:
Αν και στα δύο μέλη μιας ανίσωσης προσθέσουμε ή αφαιρέσουμε τον ίδιο αριθμό, τότε προκύπτει και πάλι μια ανισότητα με την ίδια φορά. Δηλαδή:
Αν α < β τότε α + γ < β + γ και α – γ < β – γ.
Αν α > β τότε α + γ > β + γ και α – γ > β – γ. |
Μικροπείραμα 
| 2 |
Δίνονται οι αριθμοί α και β του σχήματος.
Να συμπληρώσετε ένα από τα σύμβολα «<», «>», «=» στη θέση των κενών.
α) α.....β β) 2α.....2β γ) 5α.....5β |
Λύση
α) Ο α βρίσκεται «πιο αριστερά» από τον β, οπότε α < β.
β) Ο 2α βρίσκεται «πιο αριστερά» από τον 2β, οπότε 2α < 2β.
γ) Ο 5α βρίσκεται «πιο αριστερά» από τον 5β, οπότε 5α < 5β.
Μικροπείραμα 
| 3 |
Δίνονται οι αριθμοί α και β του διπλανού σχήματος.
Να συμπληρώσετε ένα από τα σύμβολα «<», «>», «=» στη θέση των κενών.
α) α.....β β) -2α.....-2β γ) -5α.....-5β |
Λύση
α) Ο α βρίσκεται «πιο αριστερά» από τον β, οπότε α < β.
β) Ο -2α βρίσκεται «πιο δεξιά» από τον -2β, οπότε -2α > -2β.
γ) Ο -5α βρίσκεται «πιο δεξιά» από τον -5β, οπότε -5α > -5β.
Γενικά, ισχύει για τον πολλαπλασιασμό και τη διαίρεση:
Αν και τα δύο μέλη μιας ανισότητας πολλαπλασιαστούν ή διαιρεθούν με τον ίδιο θετικό αριθμό, τότε προκύπτει και πάλι μια ανισότητα με την ίδια φορά. Δηλαδή:
 |
Αν και τα δύο μέλη μιας ανισότητας πολλαπλασιαστούν ή διαιρεθούν με τον ίδιο αρνητικόαριθμό, τότε προκύπτει και πάλι μια ανισότητα με την αντίστροφη φορά. Δηλαδή:
 |
Μικροπείραμα 
Επίλυση ανισώσεων
| 4 |
Στο διπλανό σχήμα η ζυγαριά δεν ισορροπεί! Αν ονομάσουμε x το βάρος κάθε πράσινου κύβου (τα μπλε βαρίδια ζυγίζουν 50 γραμμάρια το καθένα):
α) Με τη βοήθεια του x να εκφράσετε με μια σχέση ανίσωσης το γεγονός ότι η ζυγαριά δεν ισορροπεί.
β) Τι μπορούμε να πούμε για το βάρος x κάθε πράσινου κύβου; |
Λύση
α) Στον 1ο δίσκο της ζυγαριάς υπάρχουν 3 πράσινοι κύβοι και δύο βαρίδια των 50 γραμμαρίων, δηλαδή συνολικό βάρος 3x + 2 • 50 = 3x + 100 γραμμάρια.
Στον 2ο δίσκο υπάρχει 1 πράσινος κύβος και 8 βαρίδια των 50 γραμμαρίων δηλαδή, συνολικό βάρος
x + 8 • 50 = x + 400 γραμμάρια.
Ο 1ος δίσκος είναι πιο βαρύς, οπότε ισχύει: 3x + 100 > x + 400.
β) Η ανισότητα αυτή που περιέχει τον άγνωστο χ λέγεται ανίσωση. Για να βρούμε τον χ ακολουθούμε παρόμοιο τρόπο με αυτόν που ακολουθήσαμε για την επίλυση εξισώσεων.
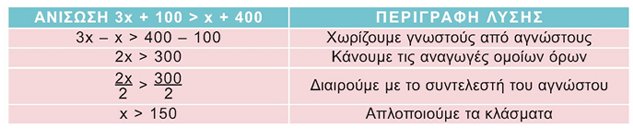
Μπορούμε να παρατηρήσουμε ότι, από την ανίσωση που βρήκαμε (x > 150) δεν μπορούμε να συμπεράνουμε πόσο ακριβώς ζυγίζει κάθε πράσινος κύβος, συμπεραίνουμε όμως ότι το βάρος του είναι οπωσδήποτε μεγαλύτερο από 150 γραμμάρια. Μπορεί να είναι 150,1 γραμμάρια, μπορεί να είναι 200 γραμμάρια ή μπορεί να είναι 1.000 κιλά! Δηλαδή, όταν λύνουμε μία ανίσωση, συνήθως δε βρίσκουμε μία μόνο λύση, αλλά άπειρες! Γι' αυτό παριστάνουμε αυτές τις λύσεις στην ευθεία των αριθμών, όπως φαίνεται στο παρακάτω σχήμα.

Το λευκό κυκλάκι πάνω ακριβώς από το 150 δείχνει ότι ο αριθμός αυτός δεν είναι λύση της ανίσωσης.
Μικροπείραμα 
Μια ανισότητα που περιέχει έναν άγνωστο x, λέγεται ανίσωση με έναν άγνωστο.
|
Ο τρόπος που ακολουθούμε για να λύσουμε μια ανίσωση, είναι παρόμοιος με τον τρόπο που ακολουθούμε στην επίλυση εξισώσεων. Δηλαδή:
 |
Χωρίζουμε γνωστούς από αγνώστους. |
 |
Κάνουμε αναγωγές ομοίων ορων. |
 |
Διαιρούμε με το συντελεστή του αγνώστου. Αν ο συντελεστής είναι θετικός η ανισότητα δεν αλλάζει φορά, ενώ αν είναι αρνητικός πρέπει να αλλάξουμε τη φορά της ανίσωσης. |
|