Εξισώσεις
|
||||||||||||||||||||||||||||||
Εξισώσεις Σε αυτή τη θεματική ενότητα θα ασχοληθούμε με τις εξισώσεις. Με άλλα λόγια, με τη χρήση γραμμάτων ή συμβόλων στη θέση ενός αριθμού που δεν γνωρίζουμε Από την 8η χιλιετία π.Χ. οι κάτοικοι της Μεσοποταμίας, πολύ πριν από τους Σουμέριους, χρησιμοποιούσαν ένα σύστημα αριθμητικής καταγραφής βασισμένο σε μικρές πήλινες «μάρκες». Από εκεί πληροφορούμαστε ότι χρησιμοποιούσαν αριθμητικές μεθόδους πολύ πιο εξελιγμένες από την απλή καταμέτρηση γεωργικών προϊόντων και τους απλούς εμπορικούς και οικονομικούς σκοπούς της εποχής τους. Βρέθηκαν στις «μάρκες» προβλήματα της εποχής εκείνης που απαιτούν τη χρήση εξισώσεων για την επίλυσή τους. Χαρακτηριστικό είναι το παρακάτω πρόβλημα. Βρήκα μια πέτρα. Δεν (τη) ζύγισα. Αφαίρεσα το ένα έβδομο. Πρόσθεσα το ένα ενδέκατο. Αφαίρεσα το ένα δέκατο τρίτο. (Τη) ζύγισα. Ποιο ήταν το αρχικό βάρος της πέτρας; Φαίνεται πως τα Μαθηματικά ήταν για τους κατοίκους της Μεσοποταμίας ένα απαραίτητο εργαλείο με το όποιο μπορούσαν να αποκρυπτογραφήσουν τις κινήσεις του Ουρανού και μια γλώσσα με την οποία μπορούσαν να επικοινωνήσουν και να καταλάβουν τους θεούς τους. |
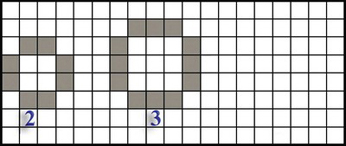
Στο διπλανό σχήμα σχεδιάσαμε σε μιλιμετρέ χαρτί το γράμμα «Ο» σε δύο μεγέθη. Ανάλογα με την πλευρά του καθενός τα ονομάσαμε μέγεθος 2 και μέγεθος 3.
Πήγα σε ένα γαλακτοκομικό αγρόκτημα και αγόρασα γάλα σε ένα δοχείο 10 λίτρων. Το δοχείο δεν χωράει στο ψυγείο μου. Έτσι θέλω να το μεταγγίσω σε δοχεία των 2 λίτρων. 
|
Έχουμε μάθει ότι μια αριθμητική παράσταση περιέχει αριθμούς και πράξεις. Από τις προηγούμενες δραστηριότητες διαπιστώνουμε ότι μπορεί να περιέχει και γράμματα.
Εφαρμογή 1η Eπιλέγω μεταβλητή «Στη γιορτή είχαμε 4 γλυκά που έφερε η Φρόσω, 10 που έφερα εγώ και αυτά που έφερε η Σοφία. Τα έφαγαν όλα!» Να εκφράσετε με μια αριθμητική παράσταση τον αριθμό των γλυκών που έφαγαν στη γιορτή. 
Λύση Οποιοδήποτε γράμμα (ή σύμβολο) μπορεί να χρησιμοποιηθεί ως μεταβλητή και μια μεταβλητή μπορεί να χρησιμοποιηθεί στη θέση οποιουδήποτε αριθμού. Για να εκφράσουμε μια φράση με αριθμητική παράσταση ακολουθούμε τρία βήματα: 1. Προσδιορίζουμε την άγνωστη ποσότητα. 2. Επιλέγουμε μια μεταβλητή για την άγνωστη ποσότητα. 3. Προσδιορίζουμε τις πράξεις ανάμεσα στους αριθμούς και τη μεταβλητή. Στη συγκεκριμένη φράση: 1. Έχουμε έναν άγνωστο: τα γλυκά που έφερε η Σοφία.. 2. Επιλέγουμε σ = τα γλυκά της Σοφίας. 3. Έφαγαν τα γλυκά της Σοφίας, συν 4, συν 10. Άρα έφαγαν σ + 4 + 10, δηλαδή σ + 14. Θα μπορέσουμε να υπολογίσουμε την τιμή της παράστασης όταν μάθουμε τον αριθμό που αντιπροσωπεύει η μεταβλητή της. Απάντηση: Έφαγαν σ + 14, όπου σ τα γλυκά της Σοφίας.
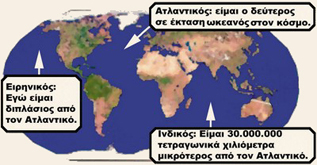
Εφαρμογή 2η Yπολογίζω τις τιμές Με βάση το σχήμα να εκφράσεις τις σχέσεις ανάμεσα στα μεγέθη των ωκεανών χρησιμοποιώντας μια μεταβλητή. Αν ο Ατλαντικός έχει έκταση 100.000.000 τετρ. χλμ. υπολόγισε την έκταση των άλλων ωκεανών. Λύση - Απάντηση 1ο βήμα: Συμβολίζω την έκταση του Ατλαντικού 2ο βήμα: Αντικαθιστώ τη μεταβλητή α με την τιμή της (100.000.000) και κάνω τις πράξεις. Eρωτήσεις για αυτοέλεγχο και συζήτηση Στο κεφάλαιο αυτό συναντήσαμε τον όρο: μεταβλητή. Χρησιμοποίησε μια μεταβλητή σε ένα δικό σου παράδειγμα.
|