Οι προηγούμενες δραστηριότητες μας βοηθούν να διαπιστώσουμε ότι πολλές φορές χρειάζεται να συγκρίνουμε φυσικούς ή δεκαδικούς αριθμούς μεταξύ τους.
Σύγκριση και διάταξη αριθμών
Δύο αριθμοί (φυσικοί ή δεκαδικοί) μπορούν πάντα να συγκριθούν μεταξύ τους.
Το αποτέλεσμα της σύγκρισης εκφράζεται με τα σύμβολα <, >, =. |
Παραδείγματα
801 < 811
1,13 < 1,15 |
Μπορούμε να διατάξουμε τους αριθμούς, σύμφωνα με το αποτέλεσμα της σύγκρισής τους, από το μικρότερο προς το μεγαλύτερο (αύξουσα σειρά) ή από το μεγαλύτερο προς το μικρότερο (φθίνουσα σειρά). |
2,05 < 3,1 < 3,5
23 > 15 >9
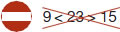
|
Η σύγκριση και η διάταξη των αριθμών μας επιτρέπει να παρεμβάλουμε έναν ή περισσότερους αριθμούς ανάμεσα σε δύο άλλους. |
1 < ... < 3

|
Εφαρμογή 1η
Ένα έτοιμο τοστ στοιχίζει 1,10 €. Για να το φτιάξουμε μόνοι μας, πρέπει να χρησιμοποιήσουμε τα εξής υλικά: ψωμί που κοστίζει 0,20 €, σαλάμι που κοστίζει 0,23 € και κασέρι που κοστίζει 0,18 €.
Σε ποια περίπτωση μας στοιχίζει το τοστ περισσότερο;
Λύση
Για να μπορέσουμε να συγκρίνουμε τα ποσά που πληρώνουμε στις δύο περιπτώσεις, πρέπει να βρούμε πόσο πληρώνουμε για όλα τα υλικά όταν το φτιάχνουμε μόνοι μας.
Έτσι έχουμε: 0,20 + 0,23 + 0,18 = .....................
Επομένως, πληρώνουμε περισσότερο όταν το αγοράζουμε έτοιμο, αφού 1,10 > .......... |
Εφαρμογή 2η
Αν τα σημεία Α και Β πάνω στην αριθμογραμμή αντιστοιχούν στους αριθμούς 2 και 6, σε ποιον αριθμό αντιστοιχεί το μέσο του τμήματος ΑΒ;

Λύση
Η απόσταση μεταξύ των σημείων Α και Β είναι 4 μονάδες. Το μέσο τους απέχει 2 μονάδες από το καθένα. Το ζητούμενο σημείο απέχει από το Α δύο (2) μονάδες, προσθέτουμε και τις 2 μονάδες που απέχει το σημείο Α από το μηδέν και βρίσκουμε: 2 + 2 = 4.
Άρα το μέσο του τμήματος ΑΒ αντιστοιχεί στον αριθμό ........... της αριθμογραμμής. |
|